图片描述
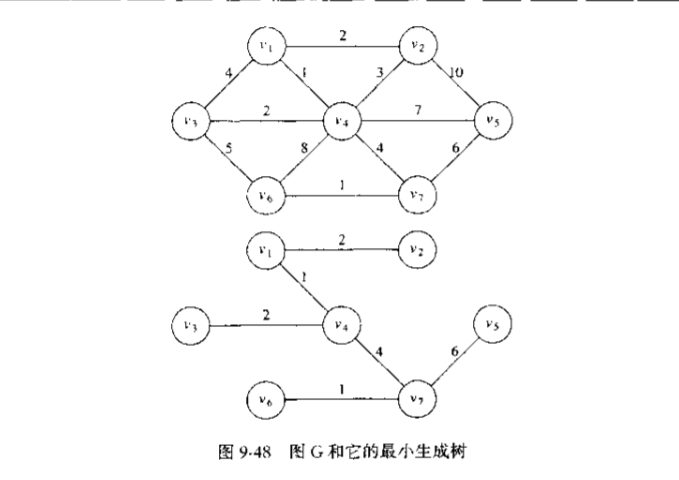
算法思想
采用贪婪策略,连续的按最小的权选择边,并且当边不产生圈时就把它作为取定的边
算法思路
问题出现
1.怎样选择最小权的边
用个排序算法
2.怎样判断加入的边是否会产生圈
(用到不相交集的知识)
判断边的两个端点是否在同一棵树中,若处于同一棵树则会产生圈
思路
1.将边的权值将边按升序排序
2.每次选择最小的边,判断两个端点是否是等价类,不是则加入这条边并且合并这两个端点
3.如此重复1-2步骤到所有边都被处理
代码实现
#include <iostream> #include <algorithm> #include <cstdlib> using namespace std; #define VERSIZE 9 //顶点数 #define MAXSIZE 15//边数 typedef struct node EDGE; typedef int Vertex; typedef int Position; struct node { Vertex start;//边起始顶点 Vertex end;//边结束顶点 int weigth;//权重 }Edge[MAXSIZE]; int VerSet[VERSIZE];//存储顶点的集合 //初始化集合 void InitSet(int VerSet[],int n) { int i = 0; for (i = 1; i <= n; i++) VerSet[i] = -1; } //读图并初始化 void ReadGraph(EDGE Edge[], int m)//边数m { int i = 0; for (i = 0; i < m; i++) { cout << "请输入第" << i+1 << "条边:"; cin >> Edge[i].start; cin >> Edge[i].end; cout << "请输入边" << "(" << Edge[i].start << "," << Edge[i].end << ")" << "的权重:"; cin >> Edge[i].weigth; } } //找出顶点在哪颗树 Position Find(int VerSet[], Vertex x) { if (VerSet[x] < 0) return x; else return VerSet[x] = Find(VerSet, VerSet[x]); } //合并两个顶点与一棵树 void Union(int VerSet[], Vertex x, Vertex y) { Vertex root1 = Find(VerSet,x); Vertex root2 = Find(VerSet,y); if (VerSet[root1] > VerSet[root2]) VerSet[root1] = root2; else { if (VerSet[root1] == VerSet[root2]) VerSet[root1]--; VerSet[root2] = root1; } } int kruskal(EDGE Edge[],int VerSet[],int m) { int sum = 0; int i = 0; for (i = 0; i < m; i++) { if (Find(VerSet, Edge[i].start) != Find(VerSet, Edge[i].end))//判断两个端点是否在同一棵树中 { Union(VerSet, Edge[i].start, Edge[i].end);//合并两个顶点 sum += Edge[i].weigth; cout << "边" << Edge[i].start << "," << Edge[i].end << endl;//输出选择的边 } } return sum; } bool compare(EDGE a,EDGE b) { return a.weigth < b.weigth; } int main() { int n = 7; int m = 12; InitSet(VerSet, n); ReadGraph(Edge, m); sort(Edge, Edge + n , compare); for (int i = 0; i < m; i++) { cout << Edge[i].weigth << " "; } cout << endl; cout << "最小生成树为:" << kruskal(Edge, VerSet, m) << endl; system("pause"); return 0; }
实验结果
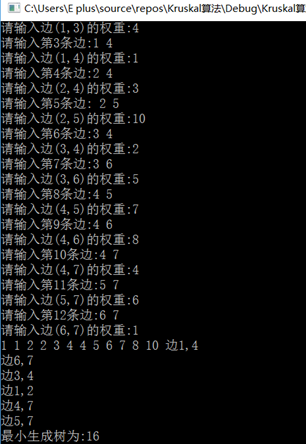
修改补充后的:SakuraOne Kruskal算法







 本文详细介绍了Kruskal算法的基本思想及其实现过程,通过贪婪策略选择边来构建最小生成树,利用排序算法和不相交集的概念确保不会形成环路。
本文详细介绍了Kruskal算法的基本思想及其实现过程,通过贪婪策略选择边来构建最小生成树,利用排序算法和不相交集的概念确保不会形成环路。
















 1863
1863

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








