POJ1330-Nearest Common Ancestors【tarjan,LCA】

最新推荐文章于 2019-11-29 01:10:50 发布

转载最新推荐文章于 2019-11-29 01:10:50 发布 · 105 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/sslwyc/p/9218522.html

本文介绍了一种使用Tarjan算法解决最近公共祖先(LCA)问题的方法。通过给出具体的代码实现，展示了如何在一个给定的树结构中找到两个节点的最近公共祖先。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

正题

题目链接：
http://poj.org/problem?id=1330

题目大意

就是给出一棵树，求LCA（最近公共祖先）

解题思路

用tarjan求LCA，这里给出tarjan算法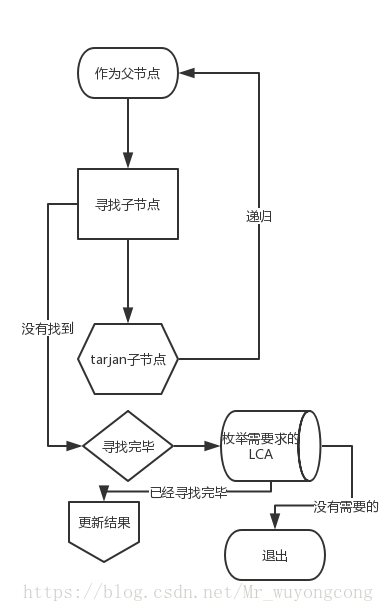
tarjan

代码

#include<cstdio>
#include<iostream>
using namespace std;
struct line{
    int next,to;
}a[20001];
int father[10001],n,m,q,p,v[10001],ans,tot,ls[10001],t,x,y,in[10001];
bool ok;
void addl(int x,int y)//加边
{
    a[++tot].to=y;
    a[tot].next=ls[x];
    ls[x]=tot;
}
int find(int x)//并查集优化
{
    return x==father[x]?x:find(father[x]);
}
void tarjan(int x)
{
    v[x]=1;
    for (int i=ls[x];i;i=a[i].next)//子节点
    {
        int y=a[i].to;
        if (v[y]) continue;
        tarjan(y);//tarjan一遍
        father[y]=x;//记录祖先
    }
    if (ok) return;//标记已找到
    if (v[q]==2 && x==p)
    {
        printf("%d\n",find(q));//输出
        ok=true;
        return;
    }
    if (v[p]==2 && x==q)///输出
    {
        printf("%d\n",find(p));
        ok=true;
        return;
    }
    v[x]=2;
}
int main()
{
    scanf("%d",&t);
    for (;t;t--)
    {
        scanf("%d",&n);
        tot=0;ok=0;
        for (int i=1;i<=n;i++){
            ls[i]=0;father[i]=i;v[i]=0;
            in[i]=0;
        }
        for (int i=1;i<n;i++)
        {
            scanf("%d%d",&x,&y);
            in[y]++;
            addl(x,y);addl(y,x);
        }
        scanf("%d%d",&q,&p);
        for (int i=1;i<=n;i++)//寻找根
          if (in[i]==0) tarjan(i);
        //printf("%d\n",ans);
    }
}