最大子数组的求解（包括首尾相接成环）

设计思想：首先先实现一个数组最大子数组的求法，主要用到的思想是从起始开始，当加到某一个地方和为负数的时候，那么最大子数组在这个数前面或者后面（截止到a[i]和为负，那么最大子数组存在于a[0]到a[i-1]或者a[i+1]到a[n-1]），然后实现首尾连接的环的情况，可以直接定义一个二倍长度的数组，存两遍数据，在分别从b[0]到b[n-1]中寻找n个数据的最大子数组，最后返回最大的即可。

出现的问题，解决的方案：在起初实现最大子数组的求解时，需要注意因为给予的起始值为0，所以当数据全为负数的时候，应该附加条件将其判断出来，当全是负数的时候直接找出最大的数即可，同样在首尾相接成环的时候也要加上这个判断。

源代码：

 

package Shi;

import java.util.*;

public class Shi {
	public static int max(int a,int b){
		if(a<b)return b;
		else return a;
	}
	public static int zumax(int a[],int n){
		int M=0;
		boolean p=false;
		for(int y=0;y<n;y++){
			if(a[y]>=0){
				p=true;
				break;
			}
		}	
		if(p==false){
			M=a[0];
			for(int y=0;y<n;y++){
				if(a[y]>M){
					M=a[y];
				}
			}
		}
		else{
		int i;
		int C=0;
		for(i=0;i<n;i++){
			C+=a[i];
			if(C>M){
				M=C;
			}
			if(C<0){
				C=0;
			}
		}
		}
		return M;
	}
	public static int huan(int a[],int n){
		int b[]=new int[(2*n)];
		int Max=0;
		boolean p=false;
		for(int y=0;y<n;y++){
			if(a[y]>=0){
				p=true;
				break;
			}
		}	
		if(p==false){
			Max=a[0];
			for(int y=0;y<n;y++){
				if(a[y]>Max){
					Max=a[y];
				}
			}
		}
		else{
		for(int i=0;i<n;i++){
			b[i]=a[i];
			b[i+n]=a[i];
		}
		int c[]=new int[n];
		for(int i=0;i<n;i++){
			for(int y=0;y<n;y++){
				c[y]=b[i+y];
			}
			if(Max<zumax(c,n)){
				Max=zumax(c,n);
			}
		}
		}
		return Max;
	}
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
		System.out.println("输入个数");
		int nn=input.nextInt();
		int aa[]=new int[nn];
		System.out.println("输入各个数字");
		for(int i=0;i<nn;i++){
			aa[i]=input.nextInt();
		}
		System.out.println("最大的子数组为"+zumax(aa,nn));
		System.out.println("首尾相接之后新的最大子数组为"+huan(aa,nn));
	}

}

 

 

结果截图：

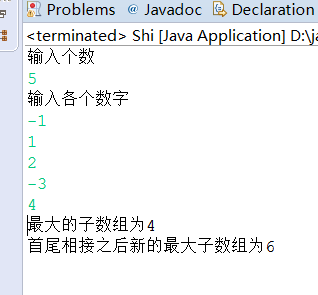
总结：整体来说，这个题目最关键的地方就是怎么实现在时间复杂度为n的情况下实现求解数组的最大子数组（这里是当和为负数的时候，最大子数组存在这个数据的前部分或者后部分）；后面实现环的情况的时候，直接定义一个二倍长度的数组即可实现。

转载于:https://www.cnblogs.com/zhaoziming/p/6649228.html