p2023

最新推荐文章于 2025-05-09 14:57:46 发布

转载最新推荐文章于 2025-05-09 14:57:46 发布 · 59 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/qywyt/p/9804594.html

终于a掉了这破题,挣扎了一上午...

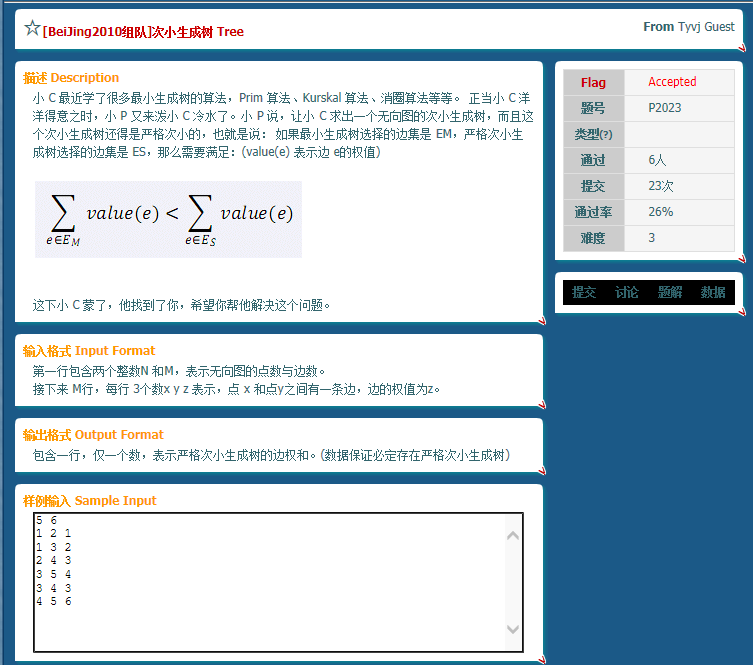
克鲁斯卡尔求最小生成树的过程是将边排序后对于所有边用并查集判断两端点是否在一个集合内,如果不在就启用这条边,将两端点连一块,否则就不用.

原理大概是根据定理:"任意一颗最小生成树一定包含无向图中权值最小的边"那么有推论"设G=(V,E)是一个连通网络,U是顶点集V的一个非空真子集.若(u,v)是G中一条"一个端点在U中(例如:u∈U),另一个端点不在U中的边(例如:v∈V-U),且(u,v)具有最小权值,则一定存在G的一棵最小生成树包括此边(u,v).

而对于一个最小生成树,枚举不在最小生成树里的边假装要加入,那么生成的新树一定要删掉在新边的两端点连线间的权值最大边.如果新边的权值就是最大边就去删最小边,因为此时删最大边的到的答案与原最小生成树边权和相同,不是严格次小生成树.

那么预处理出最小生成树后的策略就是枚举所有不在树里的边,查找两端点间最长边zui,如果o[i].v==zui就取查找次长边ci,更新答案为sum-ci+o[i].v.否则更新答案为sum-zui+o[i].v;

那么求两端点间最长边怎么搞呢?似乎可以用类似于lca的方法处理,我会树上倍增!

考虑处理lca的时候顺便处理自己与第2^k的祖先的最长边和严格次长边.最长边很简单啦,g[y][0][0]=e[i].v,g[y][k][0]=max(g[y][k-1][0],g[f[y][k-1]][0]);考虑次长边,g[y][0][1]=-inf,因为没有.

如果区间y-f[y][k-1],f[y][k-1],f[k]内部的最长边相等,次长边应该等于两个区间内部的次长边最大值,否则应该等于小的那个最长边和大的那个次长边的最长边..绕口令ing

也可以解释为:首先等于两个次长边的最大边一定没错吧.而如果两个最长边不一样长,还可以选一下最长边中小的那一个.

                g[y][k][1]=max(g[y][k-1][1],g[f[y][k-1]][k-1][1]);
                if(g[y][k-1][0]!=g[f[y][k-1]][k-1][0])
                    g[y][k][1]=max(g[y][k][1],min(g[y][k-1][0],g[f[y][k-1]][k-1][0]));

觉得难了么?一会才更难.

这样预处理完了每个点向上跳2^k次方时的最长边与次长边,求两个不一定在同一个连上的点之间的最长边与次长边该怎么办呢?比较好写的方法是跑两遍.

先处理出最长边,这个直接每次取区间内的最长边就好.(无脑取max);

            for(k=t;k>=0;k--)
                if(d[f[y][k]]>=d[x]){
                    zui=max(zui,g[y][k][0]);
                    y=f[y][k];
                }
            if(x!=y){
                for(k=t;k>=0;k--)
                    if(f[x][k]!=f[y][k]){
                        zui=max(zui,max(g[x][k][0],g[y][k][0]));
                        x=f[x][k],y=f[y][k];
                    }
                zui=max(zui,max(g[y][0][0],g[x][0][0]));
            }

而次长边的时候只要不等于最长边的边都可以取max,可以这样搞一搞

            for(k=t;k>=0;k--)
                if(d[f[y][k]]>=d[x]){
                    if(zui==g[y][k][0])
                        ci=max(ci,g[y][k][1]);
                    else
                        ci=max(ci,g[y][k][0]);
                }
            if(x!=y){
                for(k=t;k>=0;k--){
                    if(zui==max(g[x][k][0],g[y][k][0]))
                    {
                        if(g[x][k][0]==g[y][k][0])
                            ci=max(ci,max(g[y][k][1],g[x][k][1]));
                        if(g[x][k][0]>g[y][k][0])
                            ci=max(ci,max(g[x][k][1],g[y][k][0]));
                        if(g[x][k][0]<g[y][k][0])
                            ci=max(ci,max(g[x][k][0],g[y][k][1]));
                    }
                    else
                        ci=max(ci,max(g[x][k][0],g[y][k][0]));
                }
            }

看似很长,但仔细想想都是可以得到的.

然后就是码代码了.

using namespace std;
int i,k,x,y,t;
int n,m,d[100010];
int fa[100010],head[100010],tot;
bool flag[300010];
long long sum,ans;
int f[100010][20],g[100010][20][2];
int zui,ci;
inline long long min(long long a,long long b){
    return a>b?b:a;
}
inline long long max(long long a,long long b){
    return a>b?a:b;
}
struct edge{
    int  x,y,v;
    int next;
}o[300010],e[600010];
inline bool Orz(edge x,edge y){
    return x.v<y.v;
}
int get(int x){
    if(fa[x]==x)
        return x;
    return fa[x]=get(fa[x]);
}
inline void add(int x,int y,int v){
    tot++;
    e[tot].x=x;
    e[tot].y=y;
    e[tot].v=v;
    e[tot].next=head[x];
    head[x]=tot;
}
int main()
{
    n=read(),m=read();
    for(i=1;i<=m;i++)
        o[i].x=read(),o[i].y=read(),o[i].v=read();
    sort(o+1,o+1+m,Orz);
    for(i=1;i<=n;i++)
        fa[i]=i;
    for(i=1;i<=m;i++){
        x=get(o[i].x),y=get(o[i].y);
        if(x!=y){
            fa[x]=y;
            flag[i]=1;
            sum+=o[i].v;
            add(o[i].x,o[i].y,o[i].v);
            add(o[i].y,o[i].x,o[i].v);
            ans++;
            if(ans==n-1)
                break;
        }
    }
    ans=INF;
    queue<int> q;
    t=log2(n*1.0)+1;
    q.push(1);d[1]=1;
    while(q.size()){
        x=q.front();
        q.pop();
        for(i=head[x];i;i=e[i].next){
            y=e[i].y;
            if(d[y])continue;
            q.push(y);
            d[y]=d[x]+1;
            f[y][0]=x;
            g[y][0][0]=e[i].v;
            g[y][0][1]=-inf;
            for(k=1;k<=t;k++){
                f[y][k]=f[f[y][k-1]][k-1];
                g[y][k][0]=max(g[y][k-1][0],g[f[y][k-1]][k-1][0]);
                g[y][k][1]=max(g[y][k-1][1],g[f[y][k-1]][k-1][1]);
                if(g[y][k-1][0]!=g[f[y][k-1]][k-1][0])
                    g[y][k][1]=max(g[y][k][1],min(g[y][k-1][0],g[f[y][k-1]][k-1][0]));
            }
            
        }
    }
    for(i=1;i<=m;i++){
        if(!flag[i]){
            zui=ci=-inf;
            x=o[i].x,y=o[i].y;
            if(d[x]>d[y])swap(x,y);
            for(k=t;k>=0;k--)
                if(d[f[y][k]]>=d[x]){
                    zui=max(zui,g[y][k][0]);
                    y=f[y][k];
                }
            if(x!=y){
                for(k=t;k>=0;k--)
                    if(f[x][k]!=f[y][k]){
                        zui=max(zui,max(g[x][k][0],g[y][k][0]));
                        x=f[x][k],y=f[y][k];
                    }
                zui=max(zui,max(g[y][0][0],g[x][0][0]));
            }
            if(o[i].v>zui){
                ans=min(ans,sum-zui+o[i].v);
                continue;
            }
            x=o[i].x,y=o[i].y;
            if(d[x]>d[y])swap(x,y);
            for(k=t;k>=0;k--)
                if(d[f[y][k]]>=d[x]){
                    if(zui==g[y][k][0])
                        ci=max(ci,g[y][k][1]);
                    else
                        ci=max(ci,g[y][k][0]);
                }
            if(x!=y){
                for(k=t;k>=0;k--){
                    if(zui==max(g[x][k][0],g[y][k][0]))
                    {
                        if(g[x][k][0]==g[y][k][0])
                            ci=max(ci,max(g[y][k][1],g[x][k][1]));
                        if(g[x][k][0]>g[y][k][0])
                            ci=max(ci,max(g[x][k][1],g[y][k][0]));
                        if(g[x][k][0]<g[y][k][0])
                            ci=max(ci,max(g[x][k][0],g[y][k][1]));
                    }
                    else
                        ci=max(ci,max(g[x][k][0],g[y][k][0]));
                }
            }
            ans=min(ans,sum-ci+o[i].v);
        }
    }
    cout<<ans;
}