背包问题1

最新推荐文章于 2025-09-10 15:24:29 发布

转载最新推荐文章于 2025-09-10 15:24:29 发布 · 92 阅读

1 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/DYP123456/p/3471402.html

文章标签：

#数据结构与算法

本文提出了一种针对两艘货船装载问题的穷举算法，通过构建二叉子集树来寻找所有可能的装载方案，使得第一艘货船尽可能装满，同时确保所有货物能够被装载。相较于传统的穷举法，此算法利用位运算减少了不必要的计算。

先放一个基于背包问题原型的问题：

有两艘货船需要装运N个货箱，第一艘货船的载重量是C1，第二艘为C2，Wi为货箱i的重量，且W1+W2+W3+...Wn<=C1+C2,希望确定是否有一种可将所有N个货箱全部装船的方法，如果有，找出该方法。

分析：

作为背包问题，通常采用的方法有穷举（需要知道货箱的个数），动态规划，分支界限搜索算法，本章讨论结合子集树特征的一种穷举算法

题目要求W1+W2+W3+...Wn<=C1+C2，即要求在总货重不超过C1+C2这一前提下，尽可能的把货船C1装满，于是问题可以转变为：确保W1+W2+W3+...Wn<=C1+C2前提下，有多少种选择装船的方法使得C1装满。

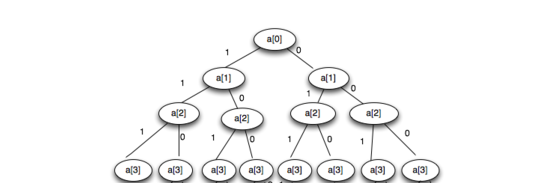
子集树的特征：在于对于一个节点的两路分支只有选择与不选择的情况，通常选择左分支为选择，计数为1，反之选择右分支为不选，计数为0；当把所有节点按照上述规则形成一颗二叉树时，通过对树的每次根到叶子节点的遍历，便可得到当前选择的选择情况。

图1 二叉子集树

回到问题，该问题如果采用分支界限搜索算法，意味着会间接的构造一颗二叉子集树，并预先通过条件判断来去除部分不可能选择，如果采用常规穷举，在已知个数N的情况下，会产生N重的循环来逐一求解

对于图1，如果把所有的情况按照选择或者不选择，把相对应的选择号记录下来，则会有这一结果：

000，001，010，011，100，101，110，111

转换为对应的十进制数则为：

0，1，2，3，4，5，6，7

结合上面的结果，不难发现，如果有N个点进行构建二叉子集树，便会有2∧N种选择情况，所需要的结果也在[0，2∧N-1]这一范围中获取

改进常规穷举算法：

通过分析可以知道，问题的所需结果在[0，2∧N-1]这一范围中获取，那么可以设计出算法的框架原型

count=2<<num-1;//count为所有选择的总计，num为货箱的个数

while(count>=0)

｛

j=count;

for(i=num;i>0;i--)//N个货物只用比较2∧N-1次，每次移位只需向右移动N个
{

k+=(j&0x01)*(*b);//将当前选择的数的二进制最后一位取出，并与数组中当前货物相乘

            if(k==c1)//当前重量达到第一艘货船的重量
            {
              print(输出结果);
                break;
            }
            else if(k>c1)//当前重量超过第一艘货船的重量
            {
                k-=*b;//去除当前的这次重量
                break;
            }
            else//当前重量未达到第一艘货船的重量
            {
                j>>=1;//当前数值右移一位
                b++;//指向数组指针移向下一个元素的地址
                continue;
            }

}

     if(k<c1&&(weight-k)<=c2)//当前选择使得第一艘货船没有装满
    {
        print(输出结果);
    }
    count--;当前选择数减1
｝

算法分析：

相比于常规的穷举算法，该算法的用到了二重循环，外层循环为选择数的总数，内层为每一个选择数移位运算的次数（N个货箱只需向右移位N位）

时间复杂度取决于货箱N的个数，即时间仍复杂度为O(2∧N)*N，当N的个数趋近于无穷大时，算法仍然不能解决（取决于计算机能表示的二进制的位数）

附录：完整C代码（WIN 8.1 64位已在VC6.0下通过）

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define n 4
int search(const int const *,int,int,int);
int main(void)
{
    int i,c1,c2,a[n];
    printf("请输入第一个货船最大载重量：");
    scanf("%d",&c1);
    printf("请输入第二个货船最大载重量：");
    scanf("%d",&c2);
    for(i=0;i<n;i++)
    {
        printf("输入%d个货物重量:",i+1);
        scanf("%d",&a[i]);
    }
    
    search(a,c1,c2,n);    
    return EXIT_SUCCESS;
}
int search(const int const *a,int c1,int c2,int num)
{
    int count,i,j,k,flag,weight,*b;
    clock_t start,end;
    flag=1,weight=0;
    start=clock();
    for(i=0,b=(int *)a,count=0;i<num;i++,b++)
    {    
        weight+=*b;
        if(weight>c1+c2)
        {
            flag=0;
            printf("货物总重量大于货船能够载重!\n");
            break;
        }
    }
    if(flag!=0)
    {
        count=2<<num-1;
        while(count>=0)
        {
            j=count;
            k=0;
            b=(int *)a;
            for(i=n;i>0;i--)
            {    
                k+=(j&0x01)*(*b);
                if(k==c1)
                {
                    printf("%d\t",count);
                    printf("1.第一个船装%d\t",k);
                    printf("2.第二个船装%d\n",weight-k);
                    break;
                }
                else if(k>c1)
                {
                    k-=*b;
                    break;
                }
                else
                {
                    j>>=1;
                    b++;
                    continue;
                }
            }
            if(k<c1&&(weight-k)<=c2)
            {
                printf("%d\t",count);
                printf("3.第一个船装%d\t",k);
                printf("4.第二个船装%d\n",weight-k);
            }
            count--;
        }
    }
    end=clock();
    printf("\n%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return flag;
}