题目链接:
题意:
\(n*m\)的矩阵使每个\(n*n\)矩阵里面准确包含\(k\)个点,问你有多少种放法。
\((1 ≤ n ≤ 100; n ≤ m ≤ 10^{18}; 0 ≤ k ≤ n^2)\)
题解:
- Let \(s_i\) number of points in the column \(i\).
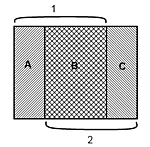
- Two neighboring squares are drawn at this picture, \(A\) is the number of point it the left area (it is one column), \(B\) is the number of points in the middle area and \(C\) is the number of points in the right area (it is one column too). That's why by definition we ###have:
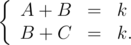
- Therefore \(A = C\).
- That's why 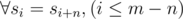
- Divide all columns by equivalence classes on the basis of \(i \mod n\) . For all \(a\) and \(b\) from one class \(s_a = s_b\).
cnta is number of columns in class with 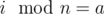
- There are \(C(n,k)^{cnt_a}\) ways to draw \(k\) points in the each of columns in the class \(a\) independendently of the other classes.
- \(dp[i][j]\) is number of ways to fill all columns in classes \(1, ... i\) in such way that .
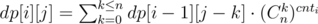
- \(cnt_i\) take only two values 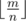 and
and 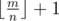
. Let's calc \(C(n,a)^{cnt_i}\) for all \(a\) and \(cnt_i\) and use it to calc our dp. We have \(O(n^2·k)\) complexity.
代码:
#include<bits/stdc++.h>
#pragma GCC optimize ("O3")
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
using namespace std;
const int N = 123;
const int K = 10000+1230;
ll pow1[N],pow2[N];
ll dp[N][K];
ll c[N][N];
//n*m的矩阵使每个n*n矩阵里面准确包含k个点,问你有多少种放法。
ll quick_pow(ll a,ll b)
{
ll tmp=a;
ll ans=1;
while(b)
{
if(b&1) ans=(ans*tmp)%mod;
tmp=(tmp*tmp)%mod;
b>>=1;
}
return ans;
}
int main()
{
int n,k;
ll m;
cin>>n>>m>>k;
for(int i=0;i<=n;i++) c[i][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
for(int i=0;i<=n;i++)
{
pow1[i]=quick_pow(c[n][i],m/n);
pow2[i]=(pow1[i]*c[n][i])%mod;
}
dp[0][0]=1;
ll now;
for(int i=0;i<n;i++)
{
for(int j=0;j<=k;j++)
{
if(dp[i][j]!=0)
{
for(int p = 0;p <= n && j + p <= k;p++)
{
if(i<m%n) now=pow2[p];
else now=pow1[p];
dp[i+1][j+p]=(dp[i+1][j+p]+dp[i][j]*now)%mod;
}
}
}
}
cout<<dp[n][k]<<endl;
return 0;
}
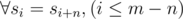
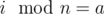
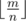 and
and 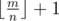







 本文探讨了一个关于在特定矩阵中放置点的计数问题。给定一个n*m的矩阵,目标是在每个n*n的子矩阵中精确放置k个点,并计算所有可能的放置方式的数量。文章提供了详细的解题思路及C++实现代码。
本文探讨了一个关于在特定矩阵中放置点的计数问题。给定一个n*m的矩阵,目标是在每个n*n的子矩阵中精确放置k个点,并计算所有可能的放置方式的数量。文章提供了详细的解题思路及C++实现代码。

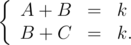
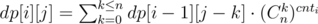

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








