UVA-221 Urban Elevations（离散化）

题意：

给出建筑左下角的坐标和建筑的宽度（w）、高度（h）、长度（d），判断从南往北看，哪些建筑可以能够看到。

思路：

将建筑的左边界和右边界用一个x数组保存下来，然后按照题目要求进行排序、去重。

这样处理之后的x数组中相邻两个数表示的区间是从南往北可以看到的。

枚举每一个建筑，然后在这个建筑的基础上枚举每一个可以看到的区间，在这基础上在枚举判断这个建筑是不是被其他的建筑给挡住了，没有就输出这个建筑的id。

 

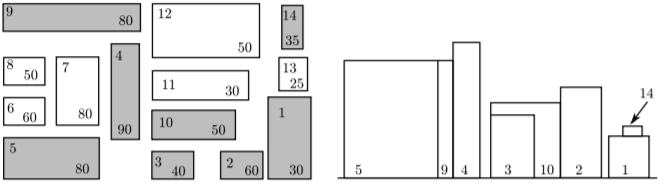
看图可以理解对x数组进行排序去重的操作。

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define MAX 1e9;
#define FRE() freopen("in.txt","r",stdin)
#define FRO() freopen("out.txt","w",stdout)
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
const int maxn = 300;
struct Build{
    double x,y,w,d,h;
    int id;
    bool operator<(const Build& bb)const{
        return x<bb.x || (x==bb.x && y<bb.y);
    }
}b[maxn];
double x[2*maxn];
int n;

bool Cover(int idx, double mx){//判断这个建筑的宽度内有没有这个中点mx
    return b[idx].x<=mx && (b[idx].x+b[idx].w)>=mx;
}

bool Visiable(int idx, double mx){
    if(!Cover(idx,mx))return false;//如果这个建筑的宽度内没有这个中点，就直接返回看不到
    for(int i = 0; i<n; i++){
        if(b[i].y<b[idx].y && b[i].h>=b[idx].h && Cover(i,mx)){
            return false;
        }
    }
    return true;
}

int main(){
    int cnt = 0;
    while(cin>>n&&n){
        for(int i = 0; i<n; i++){
            cin>>b[i].x>>b[i].y>>b[i].w>>b[i].d>>b[i].h;
            x[i*2] = b[i].x;//用x数组保存建筑的左边界
            x[i*2+1] = b[i].x+b[i].w;//用x数组保存建筑的右边界
            b[i].id = i+1;
        }
        sort(b,b+n);//对建筑按照题目的要求进行排序
        sort(x,x+2*n);//对x数组从小到大进行排序
        int m = unique(x,x+n*2)-x;//获得m个可以看到的区间，相邻的两个x数组的数表示一个区间
        if(cnt++){
            cout<<endl;
        }
        cout<<"For map #"<<cnt<<", the visible buildings are numbered as follows:"<<endl;
        cout<<b[0].id;//位于最左下角的建筑一定是可以看到的
        for(int i=1; i<n; i++){//枚举每一个建筑
            for(int j=0; j<m-1; j++){//枚举每一个可以看到的区间
                if(b[i].x>x[j] || b[i].x+b[i].w<x[j+1])continue;//如果这个建筑直接不出现在这个区间中，就直接跳过
                if(Visiable(i, (x[j]+x[j+1])/2.0)){//如果能看见就输出
                                                    //任取区间中的一个点（中点），如果建筑的宽度中有这个点
                    cout<<" "<<b[i].id;
                    break;
                }
            }
        }
        cout<<endl;
    }
    return 0;
}

View Code

 

转载于:https://www.cnblogs.com/sykline/p/10273316.html