最大子数组（1）

题目:返回一个整数数组中最大子数组的和。

要求：输入一个整形数组，数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。 求所有子数组的和的最大值。

设计思想：

　　利用动态规划的思想，将该问题转化成计算包含当前数组元素以及不包含当前数组元素的子数组之间的较大者，并向前递推，最后变成计算第一个元素和0之间的较大者，从而解决了该问题。

源代码：

1 //计算一列数组中最大子数组之和，李青，胡金辉
 2 #include<iostream>
 3 using namespace std;
 4 #define max(x,y)  ( x>y?x:y )
 5 int main()
 6 {
 7     int i,length=0,list[1000];//定义循环变量、数组长度、数组
 8     int sum1;//记录包含当前数组元素的最大子数组之和
 9     int sum2;//记录不包含当前数组元素的最大子数组之和
10     cout << "请输入数组元素：" << endl;
11         while ((cin >> list[length++] ) && getchar() != '\n');
12         cout << "你输入了" << length << "个数" << endl;
13     
14     sum1 = list[0];
15     sum2 = 0;
16     for (i = 1; i < length; i++)
17     {
18         sum2 = max(sum2, sum1);
19         sum1 = max(sum1 + list[i], list[i] );
20     }
21     sum1 = max(sum2, sum1);
22     cout << "你输入的数组中最大子数组的值为："<<sum1<<endl;
23     return 0;
24 }

结果截图：

 

 

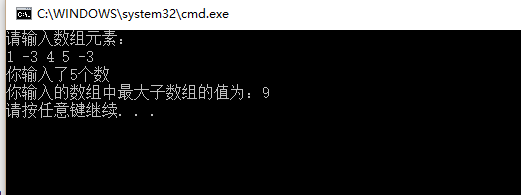
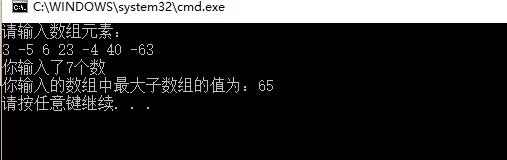
总结：

　　本次实验主要运用到了动态规划的思想，一开始并不是太清楚该思想是什么意思，后来在老师的解释下明白了，最后写出了程序，总的来说这次还是有很大收获的。

项目计划总结：

日期/任务	听课	编程	阅读相关书籍	网上查找资料	日总计
周一	100	20	10	10	140
周二		30		10	40
周三		100	30	20	150
周四	100	30			130
周五		30		20	50
周六		30	30		60
周日
周总结	200	240	70	60	570

 

时间记录日志

日期	开始时间	结束时间	中断时间	净时间	活动	备注
3/21	14：00	15：50	10	100	听课	软件工程上课
	16：00	16：20	0	20	编程
	16：30	16：40	0	10	阅读相关书籍	《构建之法》
	17：00	17：10	0	10	网上查找资料
3/22	19：00	19：30	0	30	编程
	19：40	19：50	0	10	网上查找资料
3/23	14：00	16：00	20	100	编程
	16：30	17：00	0	30	阅读相关书籍	《梦断代码》
	17：10	17：30	0	20	网上查找资料
3/24	14：00	15：50	10	100	听课	软件工程上课
	19：00	19：30	0	30	编程
3/25	19：00	19：30	0	30	编程
	20：00	20：20	0	20	网上查找资料
3/26	9：00	9：30	0	30	编程
	10:00	10:30	0	30	阅读相关书籍	《构建之法》

 缺陷记录日志：

日期	编号	类型	引入阶段	排除阶段	修复时间	备注
3/22	1	20	编码	编译	1min	未定义变量sum2
3/25	2	20	编码	编译	1min	循环嵌套输出错误

 

结对开发伙伴：李青  http://www.cnblogs.com/liqing1

工作照：

转载于:https://www.cnblogs.com/hujinhui/p/5323377.html