四则混合运算(随机生成且含括号)
git地址:https://github.com/dandan0502/arithmetic
项目完成情况
| 基本功能 | 完成情况 |
|---|---|
| 参与运算的操作数:100以内的整数,支持真分数 | √ |
| 运算符为 +, −, ×, ÷,运算符的种类和顺序必须随机生成 | √ |
| 要求能处理用户的输入,并判断对错,打分统计正确率。 | √ |
| 使用 -n 参数控制生成题目的个数 | √ |
.
| 基本功能 | 完成情况 |
|---|---|
| 支持带括号的多元复合运算 | √ |
| 运算符个数随机生成(考虑小学生运算复杂度,范围1~10) | √ |
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Pl2:16anning | 计划 | 20 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 30 |
| Development | 开发 | 1210 | 1280 |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 15 |
| · Design Spec | · 生成设计文档 | 60 | 60 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 30 | 30 |
| · Coding | · 具体编码 | 900 | 1020 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 100 |
| Reporting | 报告 | 180 | 200 |
| · Test Report | · 测试报告 | 90 | 90 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 90 |
| 合计 | 1410 | 1520 |
解题思路
刚拿到题目感觉不是特别难,也没有想的很多,主要的思路就是“随机生成四则运算式子”和“计算出结果”,其他的都是一些输入输出的问题。
整理解题思路和需要查阅资料的地方:
- 使用 -n 参数控制生成题目的个数(需查阅资料)
- 随机生成运算符个数
- 按照运算符个数随机生成运算符
- 随机生成操作数(0~100)以及真分数
- 真分数的运算和表示(需查阅资料)
- 如何对一个算式加上括号且算式合法(需查阅资料)
- 将算式转换为逆波兰式并且计算
- 键盘输入结果
- 计算总分
设计实现过程
代码组织:
本次项目采用python语言编写,一共有5个函数(包括一个主函数),分别是:
- expression()-->无参数,随机生成操作数和操作符,加入括号,返回正确的四则运算表达式
- tosuffix(expr)-->参数:四则运算中缀表达式,返回一个后缀表达式
- calculate(suffix)-->参数:后缀表达式,返回后缀表达式的值
- doMath(op,op1,op2)-->参数:op(运算符),op1(第一个操作数),op2(第二个操作数), 返回每一次的计算结果
- main(argv)-->主函数,参数:命令行参数,无返回值
函数关系:
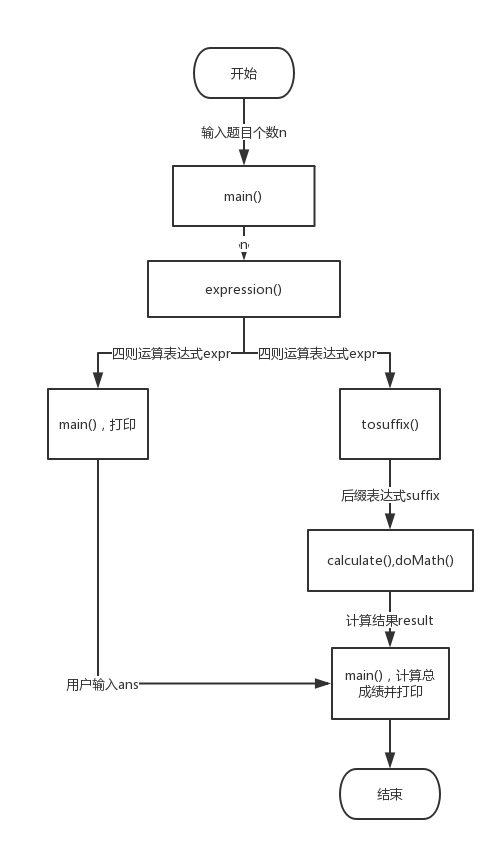
关键函数:
expression():
此函数功能是随机生成一个合法的带括号的四则运算表达式的列表,并将结果返回给主函数。其中,运算符个数、运算符、操作数都是随机生成的,括号的位置也是随机产生,最后需要判断加入括号后的表达式是否合法,若合法,则生成带括号的式子;否则,生成原始不加括号的算式。加入括号判断是否合法这个比较麻烦,主要参考了微软的破解24点的面试题的解题思路,但是因为涉及到分数运算,所以将其中部分思路进行修改。
关键函数流程图:
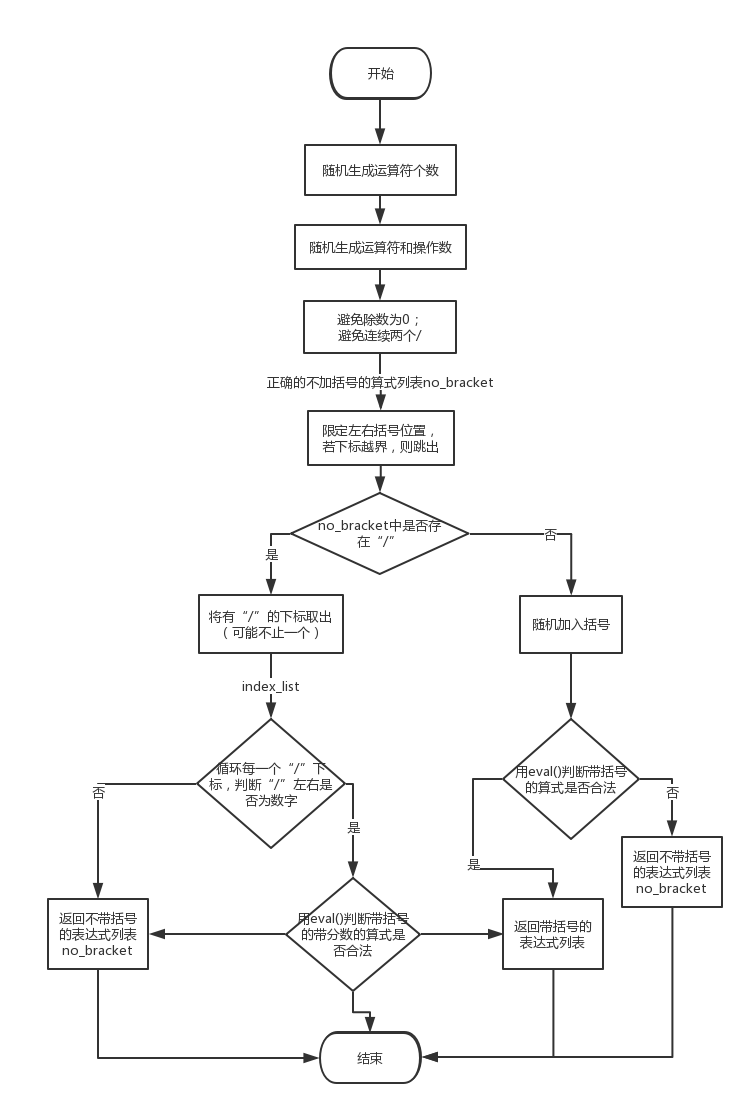
代码说明
# 主函数
def main(argv):
# 输入命令行参数设置题目个数个数
n = ''
try:
opts, args = getopt.getopt(argv,"hn:",["n="])
except getopt.GetoptError:
print ('输入格式:python filename.py -n 5')
print ('5 位为题目个数')
sys.exit(2)
for opt, arg in opts:
if opt == '-h':
print ('usage: arithmetic.py -n num of question')
sys.exit()
elif opt in ("-n", "--n"):
n = arg
# 计算成绩
each_score = float(100/int(n))
total_score = 0
flag = 0
# 输入输出
print ("本次共 {} 题,满分 100 分".format(n))
for x in range(1,int(n)+1):
expr = expression()
fomula = "".join(expr)
suffix = tosuffix(expr)
print(str(x)+". "+fomula,end = '')
ans = input()
if ans == str(calculate(suffix)):
flag+=1
print("回答正确!\n")
else:
print("回答错误!,正确答案是{}\n".format(calculate(suffix)))
print("共答对{}题".format(flag)+"," "本次得分:{}".format(round(each_score*flag)))
# 定义运算符优先级
priority = {'+':1,'-':1,'*':2,'÷':2}# 生成表达式
def expression():
opts = ['+','-','*','÷','/']
op = [] # 运算符列表
tmp = [] # 表达式列表
num_op = random.randint(1,9) # 附加功能:生成不定长运算符个数
# 生成算式
preoperand = 0
preop = ''
for i in range(num_op+1):
if preop == '÷':
preoperand = random.randint(1,20) # 防止除数为0
preop = opts[random.randint(0, 4)]
elif preop == '/':
preoperand = random.randint(1,20)
preop = opts[random.randint(0, 3)] # 防止连续两个/,如3/4/5
else:
preoperand = random.randint(0,20)
preop = opts[random.randint(0, 4)]
tmp.append(str(preoperand))
tmp.append(preop)
no_bracket = tmp.copy()
# 附加功能:加括号
try:
left1_pos = random.randint(0,len(tmp)-4) # 限定左括号位置
right1_pos = random.randint(left1_pos+3,len(tmp)-2) # 限定右括号位置
tmp.insert(left1_pos,'(')
tmp.insert(right1_pos,')')
except Exception:
no_bracket[-1] = "="
return no_bracket
flag1 = 0 # 标记是否有"/"
index_list = [] # 有/的下标列表
for i in range(len(tmp)-1):
if tmp[i] == '/':
flag1 =flag1 + 1
index_list.append(i)
# 如果没有/
if flag1 == 0:
try:
eval(("".join(tmp[:-1])).replace('÷','/'))
tmp[-1] = "="
return tmp
except Exception:
no_bracket[-1] = "="
return no_bracket
# 如果有/
else:
for i in index_list:
if tmp[i-1].isdigit() and tmp[i+1].isdigit():
try:
eval(("".join(tmp[:-1])).replace('÷','/')) #判断带括号的式子是否合法
except Exception:
no_bracket[-1] = "="
return no_bracket
else:
no_bracket[-1] = "="
return no_bracket
tmp[-1] = "="
return tmp # 把中缀表达式转为后缀表达式
def tosuffix(expr):
new_list = []
# 把分数单独作为一种操作数,使用Fraction类
i = 0
while (i<(len(expr)-1)):
if expr[i+1] == '/':
new_list.append(Fraction(int(expr[i]),int(expr[i+2])))
i = i+3
else :
new_list.append(expr[i])
i = i+1
suffix = [] # 后缀表达式
stack = [] # 操作符栈
for e in new_list:
if type(e) != str:
suffix.append(e)
elif e.isdigit(): # 操作数
suffix.append(int(e))
elif e == ')': # 右括号
tmp_pop = ''
while tmp_pop != '(':
tmp_pop = stack.pop()
if tmp_pop != '(':
suffix.append(tmp_pop)
elif len(stack) == 0 or stack[-1] == '(' or e == '(': # 左括号
stack.append(e)
else: #其他运算符
while(len(stack) and stack[-1] != '(' and priority[stack[-1]] >= priority[e]): # stack[-1] == '('和 stack[-1] != '(' 保证可变优先级
suffix.append(stack.pop())
stack.append(e)
while len(stack): # 把栈弹干净
suffix.append(stack.pop())
return suffix# 后缀表达式求值
def calculate(suffix):
calStack = []
for s in suffix:
if type(s) == int:
calStack.append(int(s))
elif type(s) != str:
calStack.append(s)
else:
operand2 = calStack.pop()
operand1 = calStack.pop()
result = doMath(s,operand1,operand2)
calStack.append(result)
return calStack.pop()
# 基本运算
def doMath(op,op1,op2):
if op == '+':
return op1+op2
elif op == '-':
return op1-op2
elif op == '*':
return op1*op2
elif op == '÷':
return Fraction(op1,op2)运行结果
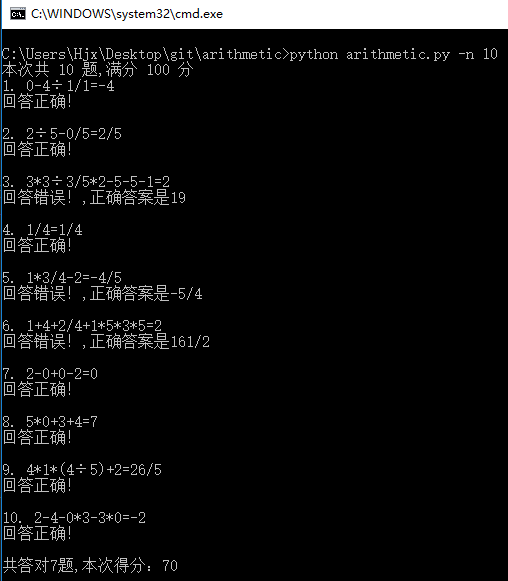
单元测试
相关知识
《构建之法》的第二章展示了好的单元测试的标准:
- 单元测试应该在最基本的功能/参数上验证程序的正确性
- 单元测试必须由最熟悉代码的人(程序的作者)来写
- 单元测试过后,机器状态保持不变
- 单元测试要快
- 单元测试可以产生可重复、一直的结果
- 独立性——单元测试的运行/通过/失败不依赖于别的测试,可以人为构造数据,以保持单元测试的独立性
- 单元测试应该覆盖所有代码路径
- 单元测试应该集成到自动测试的框架中
- 单元测试必须和产品代码一起保存和维护
测试思路
主要是对expression()、tosuffix()和calculate()这三个函数进行测试。
其中,由于expression()的表达式是随机生成的,无法进行固定的单元测试,所以采用一个标记变量flag,随机10000次下列操作:首先初始化flag=0,测试生成的表达式用eval()函数产生的结果类型是否为float或int,若是,则测试通过;否则,eval()报错,即测试不通过。
其他两个函数的测试几乎包含+、-、*、÷、正负整数、分数和括号的运算,使测试覆盖率最大化。
测试代码
# 主函数
def main():
suite = unittest.TestSuite()
suite.addTest(ArithmeticTest("testExpression"))
suite.addTest(ArithmeticTest("testToSuffix"))
suite.addTest(ArithmeticTest("testCalculate"))
runner = unittest.TextTestRunner()
runner.run(suite)# 测试类
class ArithmeticTest(unittest.TestCase):
# setup
def setup(self):
pass
def testExpression(self):
# 随机10000次,用eval()函数判断表达式是否合法
for x in range(1,10000):
expr = arithmetic.expression()
result = type(eval(("".join(expr[:-1])).replace('÷','/')))
flag = 0
if result == float:
flag = 1
elif result == int:
flag = 1
self.assertEqual(flag,1)
print("test expression() pass")
def testToSuffix(self):
# 生成9条测试语句,基本覆盖+、-、*、÷、整数、分数、括号的情况
self.assertEqual(arithmetic.tosuffix(['3', '+', '12', '/', '12', '+', '12', '+', '17', '=']),[3, Fraction(1, 1), '+', 12, '+', 17, '+'])
self.assertEqual(arithmetic.tosuffix(['4', '*', '17', '/', '14', '*', '4', '+', '7', '-', '12', '/', '20', '-', '4', '+', '14', '=']),[4, Fraction(17, 14), '*', 4, '*', 7, '+', Fraction(3, 5), '-', 4, '-', 14, '+'])
self.assertEqual(arithmetic.tosuffix(['11', '/', '6', '÷', '5', '+', '0', '*', '4', '/', '6', '=']),[Fraction(11, 6), 5, '÷', 0, Fraction(2, 3), '*', '+'])
self.assertEqual(arithmetic.tosuffix(['18', '/', '15', '÷', '9', '/', '10', '*', '5', '-', '18', '*', '3', '÷', '18', '=']),[Fraction(6, 5), Fraction(9, 10), '÷', 5, '*', 18, 3, '*', 18, '÷', '-'])
self.assertEqual(arithmetic.tosuffix(['5', '+', '7', '÷', '(', '14', '-', '20', '÷', '9', '÷', '13', '÷', '7', '-', '3', '+', '12', ')', '*', '13', '=']),[5, 7, 14, 20, 9, '÷', 13, '÷', 7, '÷', '-', 3, '-', 12, '+', '÷', 13, '*', '+'])
self.assertEqual(arithmetic.tosuffix(['10', '/', '19', '÷', '9', '-', '0', '=']),[Fraction(10, 19), 9, '÷', 0, '-'])
self.assertEqual(arithmetic.tosuffix(['18', '+', '(', '13', '+', '18', '*', '4', '*', '17', ')', '*', '3', '+', '19', '/', '20', '-', '14', '*', '5', '=']),[18, 13, 18, 4, '*', 17, '*', '+', 3, '*', '+', Fraction(19, 20), '+', 14, 5, '*', '-'])
self.assertEqual(arithmetic.tosuffix(['0', '/', '6', '-', '12', '*', '(', '8', '/', '2', ')', '+', '16', '=']),[Fraction(0, 1), 12, Fraction(4, 1), '*', '-', 16, '+'])
self.assertEqual(arithmetic.tosuffix(['12', '*', '(', '9', '*', '20', ')', '-', '16', '=']),[12, 9, 20, '*', '*', 16, '-'])
print("test tosuffix() pass")
def testCalculate(self):
# 生成7条测试语句,包含的结果类型覆盖正负整数和分数
self.assertEqual(arithmetic.calculate([5, Fraction(7, 9), 18, '*', '-', 18, 20, '÷', '-']),Fraction(-99,10))
self.assertEqual(arithmetic.calculate([1, 15, 19, '÷', 8, '÷', 13, '÷', 14, '*', '-', 15, 2, '*', '-']),Fraction(-28757,988))
self.assertEqual(arithmetic.calculate([18, 16, '+']),34)
self.assertEqual(arithmetic.calculate([6, Fraction(16, 11), 11, '÷', '-', 5, 10, 5, '÷', '-', 3, '÷', '+']),Fraction(831,121))
self.assertEqual(arithmetic.calculate([12, 5, '-', Fraction(5, 18), '-', Fraction(13, 5), '+']),Fraction(839,90))
self.assertEqual(arithmetic.calculate([17, 16, '*', 17, '+', 11, 16, '*', '-', 13, 11, '*', 0, '*', '+', 4, '-']),109)
self.assertEqual(arithmetic.calculate([4, Fraction(1, 1), '*', 8, '-']),-4)
print("test calculate() pass")测试结果
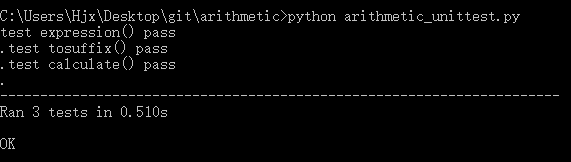
性能分析
参考http://www.cnblogs.com/waple/p/7588652.html提供的性能测试工具,随机生成10万道题。
- expression()函数性能
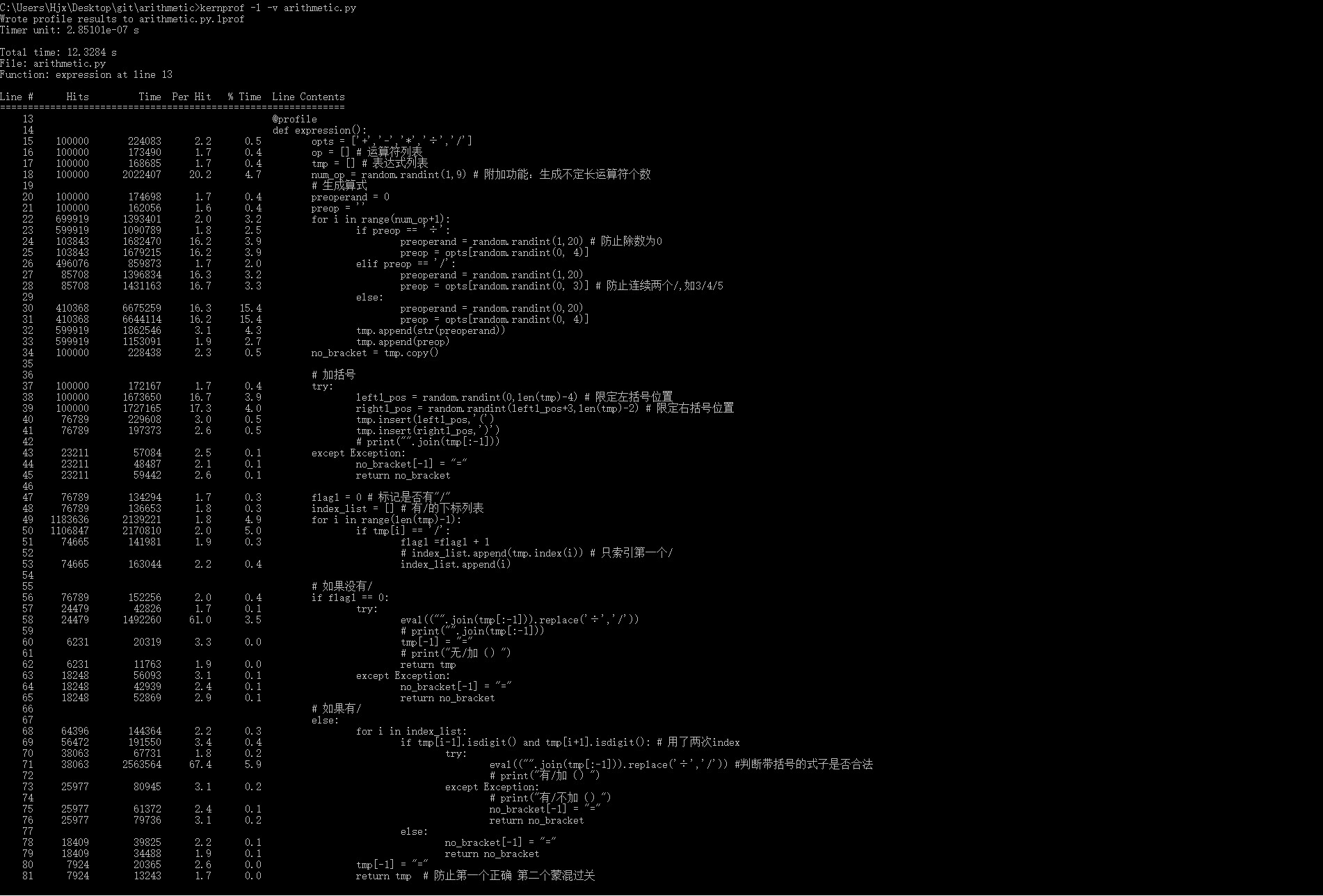
由运行结果可知,生成10万道题expression()函数共花费12.3284s,其中最耗时的语句为eval(("".join(tmp[:-1])).replace('÷','/')),猜想主要原因是在此语句中完成了列表合并、字符替换以及eval()求值这三个操作,若将其分开,应该与普通语句执行时间差不多。
- tosuffix()函数性能
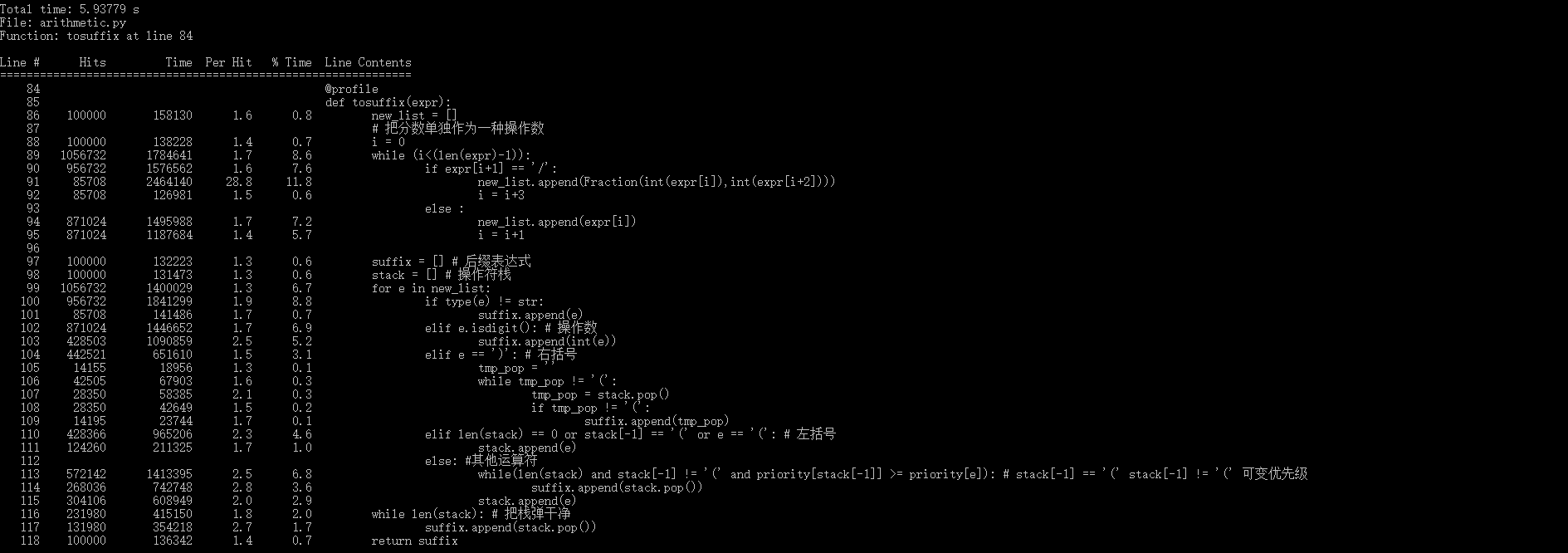
由运行结果可知,生成10万道题tosuffix()函数共花费5.93779s,其中最耗时的语句为new_list.append(Fraction(int(expr[i]),int(expr[i+2]))),猜想主要原因是此次语句中完成了列表下标索引、调用Fraction方法、生成新列表这三个操作。
- calculate()函数性能

由运行结果可知,生成10万道题calculate()函数共花费6.7123s,其中最耗时的语句为result = doMath(s,operand1,operand2),猜想主要原因是在此语句中调用doMath()方法进行计算。
从以上分析可发现,在一条语句中调用其它函数或将许多操作合成一条语句都会增加语句执行时间。初步解决方案是:可将语句拆分和将被调函数放在其他函数中,但是不能解决实际性能问题,具体改进方案准备和同学商量一下在后面完成。
项目小结
新的知识
- Fraction()-->完成分数的表示和计算,并且用分数表示出来.
- eval()-->可以自动进行四则混合运算(带括号),但是在我发现这个方法时已经将中缀转后缀表达式和计算部分写完了,所以就没有更改代码,但是在“加括号”和测试时都使用到了这个方法,感觉特别方便。
- 性能测试-->能够很方便地看到程序的运行时间及效率,对于以后的修改可以更加专业且有针对性。
- 单元测试-->测试不仅是在开发的过程中将代码跑通,而且可以发现程序隐藏的错误。
- 如何判断一个算式中加了括号的合法性-->微软面试题--24点
- 了解到了python命令行的基本用法。
- re.split()-->若一个字符串中含有不同的符号,可以直接切分,str.split()和re.split()的区别,虽然最后没有用到这个方法,但是记录在此,方便日后查阅。
一些感悟
这个项目我觉得很有意义,虽然核心算法并不是难,原理也都学过,但是还是花了不少时间来实现。分析其主要原因是平常练习不够,“眼高手低”,对于很多知识来说,只知道原理,没有动手完成过就不算真正掌握。并且,稍微加一些小的功能也需要耗费心血去完成。对于课堂上学到的和书中看到的知识也可以应用到实际的开发过程中,我觉得很实用,对它们的理解也更深刻了。接下来如果有机会,我觉得可以在新的功能如增加计时功能、开发界面等方面下功夫。
路还很长,但是我不会放弃。




 本文介绍了一个能够随机生成含括号的四则混合运算题目的Python程序,支持真分数运算,具备用户输入答案并自动判分功能。
本文介绍了一个能够随机生成含括号的四则混合运算题目的Python程序,支持真分数运算,具备用户输入答案并自动判分功能。
















 1264
1264

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








