二维数组最大连通子数组

设计思路：

对n*m的二维数组进行分解，分解为n个一维数组，再先求这n个一维数组的最大子数组和，并记下每行最大一维子数组的下标如2-5，这是就会分两种情况第一种是行之间的最大子数组是相连的，如第一行是2-5，第二行是3-6，这是直接相加就行。第二种是不相连的如第一行是2-5，第二行是6-7，这时候就把每行的最大子数组看成一个整体，再使每个最大数组块进行相连，求使其相连的最小代价。最后就可求出最大联通子数组的和。

代码：

mport java.awt.Point;  
import java.util.Scanner;  
    
public class main {  
    public static int add(int a[][],int i,int j,int k)  
    {  
        int n;  
        int b=0;  
        for(n=j;n<=i+j;n++)  
        {  
            b+=a[n][k];  
        }  
            
        return b;  
    }  
    
    public static void main(String[] args) {  
        // TODO Auto-generated method stub  
        int i,j,k,l;  
        int sum=0,s,h,e;  
        Point head=new Point();  
        Point end=new Point();  
            
            
        Scanner sc=new Scanner(System.in);  
        System.out.print("请输入矩阵的行数：");  
        int x=sc.nextInt();  
        System.out.print("请输入矩阵的列数：");  
        int y=sc.nextInt();  
        int a[][]=new int[x][y];  
        int b[]=new int[y];  
        System.out.println("请输入数组中的数：");  
        for(i=0;i<x;i++)  
        {  
            for(j=0;j<y;j++)  
            {  
                a[i][j]=sc.nextInt();  
            }  
        }  
            
        for(i=0;i<x;i++)  
        {  
            for(j=0;i+j<x;j++)  
            {  
                s=0;  
                h=0;  
                e=0;  
                for(k=0;k<y;k++)  
                {  
                    b[k]=add(a,i,j,k);  
                }  
                for(l=0;l<x;l++)  
                {  
                    s+=b[l];  
                    if(s>0)  
                    {  
                        e++;  
                    }  
                    else
                    {  
                        s=0;  
                        h=l+1;  
                        e++;  
                    }  
                    if(s>sum)  
                    {  
                        sum=s;  
                        head.x=h;  
                        head.y=j;  
                        end.x=e;  
                        end.y=i+j;  
                    }  
                }  
                if(s>0&&h!=0)  
                {  
                    l=0;  
                    e=e-x;  
                    while(s>0&&e!=h-1)  
                    {  
                        s+=b[l];  
                        l++;  
                        e++;  
                        if(s>sum)  
                        {  
                            sum=s;  
                            head.x=h;  
                            head.y=j;  
                            end.x=e;  
                            end.y=i+j;  
                        }  
                    }  
                }  
            }  
        }  
    
        System.out.print("最大子数组的和为:");  
        System.out.println(sum);  
        System.out.println("最大子数组为:");  
        if(end.x>head.x)  
        {  
            for(i=head.y;i<=end.y;i++)  
            {  
                for(j=head.x;j<end.x;j++)  
                {     
                    System.out.print(a[i][j]);  
                    System.out.print(" ");  
                }  
                System.out.println();  
            }  
                
        }  
        else
        {  
            for(i=head.y;i<=end.y;i++)  
            {  
                for(j=head.x;j<x;j++)  
                {  
                    System.out.print(a[i][j]);  
                    System.out.print(" ");  
                }  
                for(j=0;j<end.x;j++)  
                {  
                    System.out.print(a[i][j]);  
                    System.out.print(" ");  
                }  
                System.out.println();  
            }  
                
        }  
            
    }  
       
}

总结：

学会转换思路，讲一个大问题转换为几个小问题，慢慢的解决，一块一块的解决。

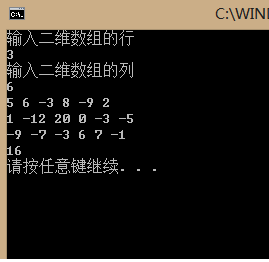
截图：

转载于:https://www.cnblogs.com/dyc940210/p/4594429.html