As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.
Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?
You have to determine the winner of the game for all initial positions of the marbles.
The first line of input contains two integers n and m (2 ≤ n ≤ 100,  ).
).
The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from v to u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.
Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.
4 4
1 2 b
1 3 a
2 4 c
3 4 b
BAAA
ABAA
BBBA
BBBB
5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h
BABBB
BBBBB
AABBB
AAABA
AAAAB
题意:给你一个有向无环图,两个人玩游戏,规则是A先走然后B走,附加条件是走的第i步的那条边的权值要大于等于上一步边的权值,然后输出A,B所有起点的共n*n种情况的胜负。
我的做法是从末端考虑,相当于进行拓扑,把所有出度为0的点放入到一个own已有队列中,每当有一个新的出度为0的点进入时,就把这个点和其它所有点所组成的情况进行dp,就是枚举这个点的
下一步情况,然后再枚举另一个点的下一步情况,相当于两个for循环,同时为应对附加条件要对走的起点边进行记录,所以开三维dp,因为是倒着向前推得,所以记录的是起点边,更新的时候就
把小于等于起点边的同时也更新掉,第三位的意思是小于等于即可利用这个。。。
然后别人的做法是直接从头往后走就ok了,然后记忆化记忆一下,比我的优美多了。。。
#include<cstdio> #include<vector> #include<cstring> #include<algorithm> using namespace std; const int N=105; int dp[N][N][200],n,ru[N],m,q[N],own[N]; vector<int>F[N]; vector<pair<int,int> >Z[N]; int main(){ scanf("%d%d",&n,&m); int x,y,l=0,r=0,tot=0;char z; for(int i=1;i<=m;++i) { scanf("%d %d %c",&x,&y,&z); Z[x].push_back(make_pair(y,(int)z)); F[y].push_back(x); ++ru[x]; } for(int i=1;i<=n;++i) if(!ru[i]) q[r++]=i; while(l<r) { int u=q[l++]; for(int i=0;i<tot;++i) for(int j=0;j<(int)Z[u].size();++j) { bool ok=1; for(int k=0;k<(int)Z[own[i]].size();++k) if(Z[own[i]][k].second>=Z[u][j].second) ok&=dp[Z[u][j].first][Z[own[i]][k].first][Z[own[i]][k].second]; dp[u][own[i]][Z[u][j].second]|=ok; if(ok) for(int l=(int)'a';l<=Z[u][j].second;++l) dp[u][own[i]][l]=1; } for(int i=0;i<tot;++i) for(int j=0;j<(int)Z[own[i]].size();++j) { bool ok=1; for(int k=0;k<(int)Z[u].size();++k) if(Z[own[i]][j].second<=Z[u][k].second) ok&=dp[Z[own[i]][j].first][Z[u][k].first][Z[u][k].second]; dp[own[i]][u][Z[own[i]][j].second]|=ok; if(ok) for(int l=(int)'a';l<=Z[own[i]][j].second;++l) dp[own[i]][u][l]=1; } for(int i=0;i<(int)F[u].size();++i) { int v=F[u][i]; --ru[v]; if(ru[v]==0) q[r++]=v; } own[tot++]=u; } for(int i=1;i<=n;++i) { for(int j=1;j<=n;++j) if(dp[i][j][(int)'a']) putchar('A');else putchar('B'); puts(""); } }
http://blog.youkuaiyun.com/winter2121/article/details/79203764//别人的解法
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int n,m,x,y,dp[108][108][28],dis[108][108]; int DP(int s,int t,int w){ if(dp[s][t][w-'a']>=0) return dp[s][t][w-'a']; for(int i=1;i<=n;++i) if(dis[s][i]>=w&&(DP(t,i,dis[s][i])==0)) return dp[s][t][w-'a']=1; return dp[s][t][w-'a']=0; } int main(){ char z; scanf("%d%d",&n,&m); for(int i=1;i<=m;++i) { scanf("%d %d %c",&x,&y,&z); dis[x][y]=z; } memset(dp,-1,sizeof(dp)); for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) DP(i,j,'a'); for(int i=1;i<=n;++i) { for(int j=1;j<=n;++j) printf("%c",dp[i][j][0]?'A':'B'); puts(""); } }
Here's the graph in the first sample test case:
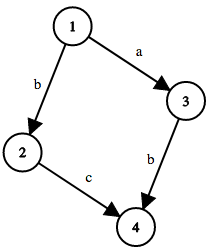
Here's the graph in the second sample test case:
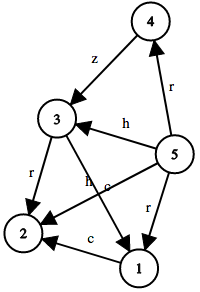







 本文介绍了一种基于有向无环图的游戏胜负判定算法。通过拓扑排序和动态规划的方法,解决了一个两人轮流移动棋子的问题,确保每一步移动后字符的ASCII值不小于前一步。最终输出所有起始位置下玩家A和B的胜负情况。
本文介绍了一种基于有向无环图的游戏胜负判定算法。通过拓扑排序和动态规划的方法,解决了一个两人轮流移动棋子的问题,确保每一步移动后字符的ASCII值不小于前一步。最终输出所有起始位置下玩家A和B的胜负情况。
















 718
718

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








