威佐夫博弈

　　威佐夫博弈（Wythoff's game）：有两堆各若干个物品，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

推导：

　　应为我们一共只有两堆石头，所以用一个二维表表示没一种状态。（如图一）

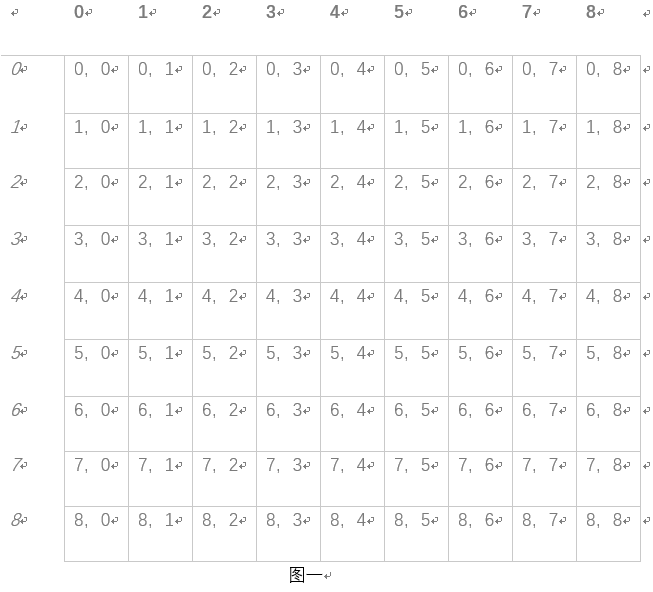
　　假设现在第一堆石头有3个，第二堆石头有5个，有两种操作方式从任一堆取至少一个或同时从两堆中取同样多的物品，则可能得到的结果如下图所示黄线所表示的区域即为可能得到的结果（如图二）

　　（3，5）这个状态又能由蓝线所表示的区域经过一次操作后达到。（如图三）

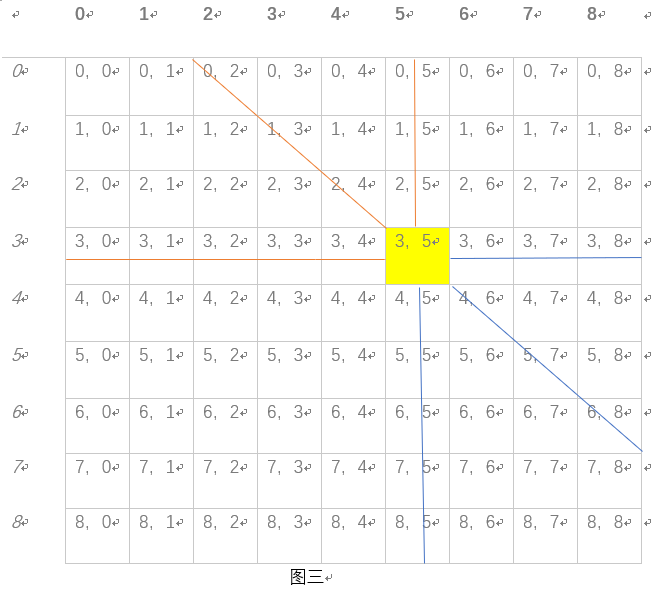
　　现在我们认为（0，0）是一种失败状态，因为上一个人已经把石子取完了，那么我们能够一步到（0，0）的状态叫做胜利态，如黄线区域所示（如图四）

 

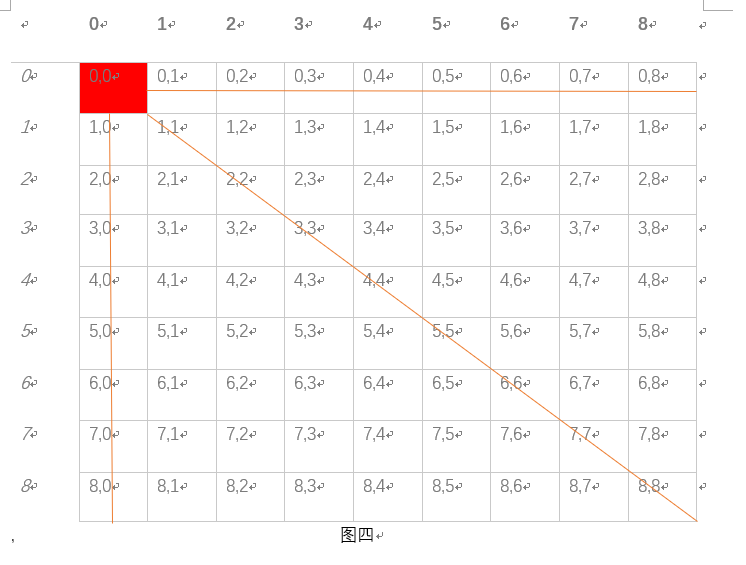
　　空出的第一个位置是（1，2），我们可以得到（1，2）是一个失败点，因为经过一次操作后他只能到达成功点（图五）

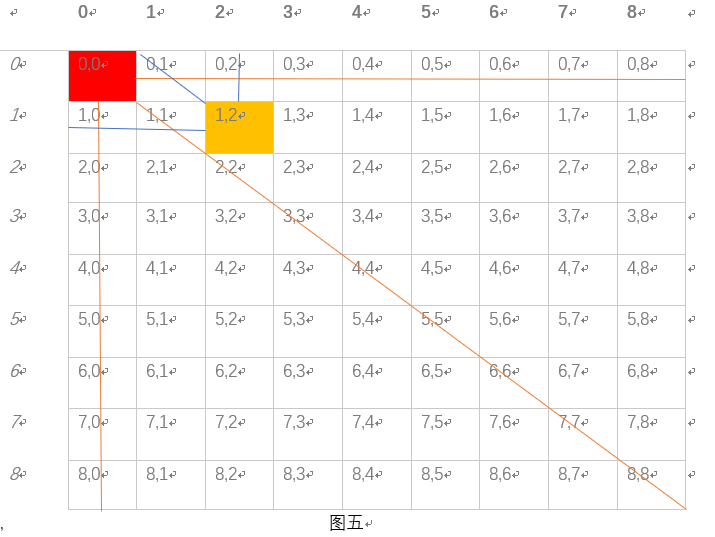
　　同理（2，1）也是一个失败点，反复进行上述操作得到下图（图六）

　　根据上图我们得到前几个必败点:(0，0)、(1，2)、(3，5)、(4，7)、(6，10)、(8，13)、(9，15)、(11，18)、(12，20)。

　　并能的到一下性质：

　　1。任何自然数都包含在一个且仅有一个奇异局势中。

　　由于ak是未在前面出现过的最小自然数，所以有a[k] > a[k-1] ，而 bk= a[k] + k > a[k-1] + k > a[k-1] + k - 1 = b[k-1] > a[k-1] 。所以性质1成立。

　　2。任意操作都可将奇异局势变为非奇异局势。

　　事实上，若只改变奇异局势(ak，bk)的某一个分量，那么另一个分量不可能在其他奇异局势中，所以必然是非奇异局势。如果使(ak，bk)的两个分量同时减少，则由于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局势。

　　3。采用适当的方法，可以将非奇异局势变为奇异局势。

　　假设面对的局势是(a,b)，若 b = a，则同时从两堆中取走 a 个物体，就变为了奇异局势(0，0);如果a = ak ，b > bk 那么，取走b - bk个物体，即变为奇异局势;如果 a = ak ， b < bk 则同时从两堆中拿走a-a[b-a] 个物体变为奇异局势( a[b-a], b-a+a[b-a]);如果a > ak ，b= ak + k 则从第一堆中拿走多余的数量a - ak 即可;如果a < ak ，b= ak + k,分两种情况，第一种，a=aj (j < k)从第二堆里面拿走 b - bj 即可;第二种，a=bj (j < k)从第二堆里面拿走 b - aj 即可。

　　4。第i个奇异点的a，b差值为i-1。

　　5。假设（x，y）为失败点且x<y,z=y-x;则x=（int）（（sqrt（5）+1）/2*z）；

转载于:https://www.cnblogs.com/wz-archer/p/10645174.html