可持久化的学习

以前我们学习了线段树可以知道，线段树的每一个节点都储存的是一段区间，所以线段树可以做简单的区间查询，更改等简单的操作。

而后面再做有些题目，就可能会碰到一种回退的操作。这里的回退是指回到未做各种操作之前的状态。

回退的时候，如果暴力点，就直接将每步所操作的线段树都存下来，然后直接翻阅回去，这种方法虽然简单，但是对空间和时间的需求太大了，肯定不能过。

所以这时候我们就可以选择可持久化操作。

可持久化是数据结构里面的一种方法，其总体就是把一个数据结构的历史状态全部都保存下来，从而能够快速的查找之前出现过的某个操作的结果，并且还可以对其继续操作。但是与直接暴力不一样，做修改的时候，每一次修改，只有一条链上的节点被修改，而其他的节点信息都没有变。因此，我们就可以只对这一次的修改操作新建包括一个新根在内的log_n个节点，其他的节点我们与上一课树共用。这样一来，我们既能保存之前的信息，又能进行修改操作。

而一般常用的数据结构里面用到的可持久化的线段树。

可持久化的线段树，又叫主席树。其思想大概就如图。在每一步的线段树操作后将改变的那一条链给单独拎出来，然后新建一次链，而没有改变的链就不动，再将新链与不动的那部分重新组合一下，就成了。

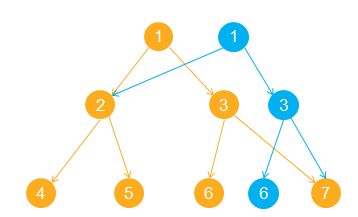
直接看模板裸题吧 https://www.luogu.org/problemnew/show/P3919

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
struct node{
  int lc,rc;
  long long int v;
}t[maxn << 8];//可持久化线段树
int root[maxn << 5];//root[i]表示版本号为i的线段树的根节点编号
long long int a[maxn];//长度为 N 的数组
int n,m;//n个点，m种操作
int tot;
 
int build(int l, int r) {
    int pos = ++tot;  //版本++ 
    if (l == r) {
        t[pos].v = a[l];  //记录这个点的值 
    }
    else{
        int mid=(l+r)>>1;
        t[pos].lc=build(l,mid); //左子树
        t[pos].rc=build(mid+1,r); //右子树 
    }
    return pos;
}

int query(int pos, int p, int l, int r) {  //查询版本pos中 a[p]的值 
    if (l == r) {
        return t[pos].v;
    }
    int mid = (l+r)>>1;
    if(p <= mid) return query(t[pos].lc, p, l, mid);
    else return query(t[pos].rc, p, mid + 1, r);
}

int update(int old, int tar, int c, int l, int r) {  //修改  a[tar] 为 c 
    int pos = ++tot; //新开节点时，需要依靠前面构建的节点编号+1
    if (l == r) {
        t[pos].v = c;
        return pos;
    }
    t[pos].lc = t[old].lc;
    t[pos].rc = t[old].rc;  // 将老树复制一份过来 

//这里也可以直接写 t[pos] = t[old] ; 

    int mid = l + (r - l)/2;
    if(tar <= mid) t[pos].lc = update(t[old].lc, tar, c, l, mid);
    else t[pos].rc = update(t[old].rc, tar, c, mid + 1, r);
    return pos;
}
 
int main(){
    while (scanf("%d %d", &n, &m) != EOF) {
        tot = 0;  //代表初始版本 
        for (int i = 1;i <= n; i++){
            scanf("%lld", &a[i]);
        }
        root[0] = build(1,n);
        int v,x,l,w;
        for (int i = 1;i <= m; i++){
            scanf("%d %d %d", &v, &x, &l);
            if (x == 1) {
                scanf("%d", &w);
                root[i] = update(root[v], l, w, 1, n);
             } 
              else {
                root[i] = root[v];
                   printf("%lld\n",query(root[v], l, 1, n));
             }
        }
      }
      return 0;
}

转载于:https://www.cnblogs.com/wushengyang/p/10519531.html