leetcode 971. 翻转二叉树以匹配先序遍历

最新推荐文章于 2024-05-01 16:52:14 发布

转载最新推荐文章于 2024-05-01 16:52:14 发布 · 72 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/zhanzq/p/11063367.html

博客围绕二叉树展开，给定有n个节点的二叉树，节点值不同且处于特定范围，可交换节点左右子节点来翻转。目标是翻转最少节点，使树的先序遍历行程与给定行程voyage匹配，若可行返回翻转节点值列表，不可行则返回空列表。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：
示例 1：
示例 2：
示例 3：
解法：

题目描述：

给定一个有 N 个节点的二叉树，每个节点都有一个不同于其他节点且处于 {1, ..., N} 中的值。

通过交换节点的左子节点和右子节点，可以翻转该二叉树中的节点。

考虑从根节点开始的先序遍历报告的 N 值序列。将这一 N 值序列称为树的行程。

（回想一下，节点的先序遍历意味着我们报告当前节点的值，然后先序遍历左子节点，再先序遍历右子节点。）

我们的目标是翻转最少的树中节点，以便树的行程与给定的行程 voyage 相匹配。

如果可以，则返回翻转的所有节点的值的列表。你可以按任何顺序返回答案。

如果不能，则返回列表[-1]。

示例 1：

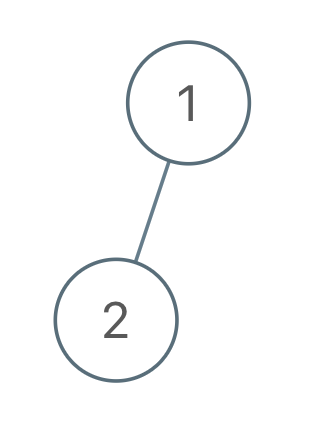
输入：root = [1,2], voyage = [2,1]
输出：[-1]

示例 2：

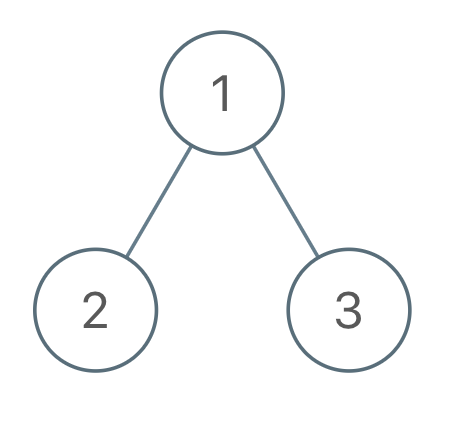
输入：root = [1,2,3], voyage = [1,3,2]
输出：[1]

示例 3：

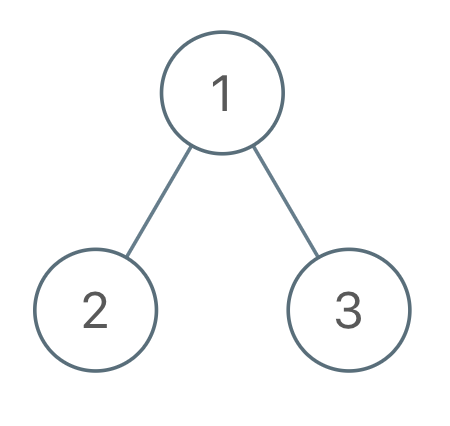
输入：root = [1,2,3], voyage = [1,2,3]
输出：[]

提示：

1 <= N <= 100

解法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> flipMatchVoyage(TreeNode* root, vector<int>& voyage) {
        if(root == NULL){
            return {};
        }else if(root->val != voyage.front()){
            return {-1};
        }else{
            voyage.erase(voyage.begin());
            if(root->left == NULL){
                return flipMatchVoyage(root->right, voyage);
            }else if(root->right == NULL){
                return flipMatchVoyage(root->left, voyage);
            }else{
                if(root->left->val == voyage.front()){
                    vector<int> left = flipMatchVoyage(root->left, voyage);
                    if(left.size() == 1 && left.front() == -1){
                        return {-1};
                    }else{
                        vector<int> right = flipMatchVoyage(root->right, voyage);
                        if(right.size() == 1 && right.front() == -1){
                            return {-1};
                        }
                        left.insert(left.end(), right.begin(), right.end());
                        return left;
                    }
                }else{
                    vector<int> left = flipMatchVoyage(root->right, voyage);
                    if(left.size() == 1 && left.front() == -1){
                        return {-1};
                    }else{
                        vector<int> right = flipMatchVoyage(root->left, voyage);
                        if(right.size() == 1 && right.front() == -1){
                            return {-1};
                        }
                        left.insert(left.end(), right.begin(), right.end());
                        left.insert(left.begin(), root->val);
                        return left;
                    }
                }
            }
        }
    }
};

转载于:https://www.cnblogs.com/zhanzq/p/11063367.html