Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
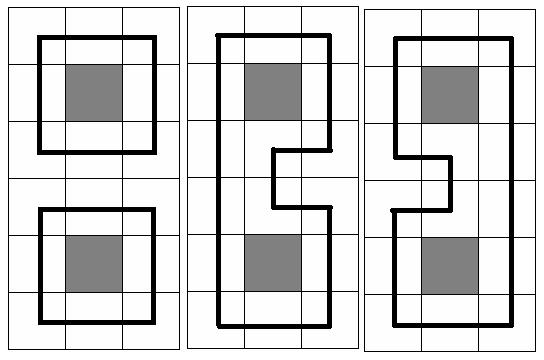
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.
题目大意:用任意多个回路覆盖矩阵上的1.
思路:插头DP,参考IOI国家集训队论文,陈丹琦的《基于连通性状态压缩的动态规划问题》
代码(62MS)(普通推,一大堆无用状态):


1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <iostream> 5 using namespace std; 6 typedef long long LL; 7 8 const int MAXN = 13; 9 10 int mat[MAXN][MAXN]; 11 LL dp[MAXN][MAXN][1 << MAXN]; 12 int n, m, T; 13 14 LL solve() { 15 memset(dp, 0, sizeof(dp)); 16 dp[0][m][0] = 1; 17 for(int i = 1; i <= n; ++i) { 18 for(int j = 0; j < (1 << m); ++j) dp[i][0][j << 1] = dp[i - 1][m][j]; 19 for(int k = 1; k <= m; ++k) { 20 for(int state = 0; state < (1 << (m + 1)); ++state) { 21 int y = 1 << k, x = y >> 1; 22 if(mat[i][k]) { 23 if((state & x) && (state & y)) { 24 dp[i][k][state] = dp[i][k - 1][state - x - y]; 25 } else if((state & x) == 0 && (state & y) == 0) { 26 dp[i][k][state] = dp[i][k - 1][state + x + y]; 27 } else dp[i][k][state] = dp[i][k - 1][state ^ x ^ y] + dp[i][k - 1][state]; 28 } else { 29 if((state & x) == 0 && (state & y) == 0) { 30 dp[i][k][state] = dp[i][k - 1][state]; 31 } else dp[i][k][state] = 0; 32 } 33 } 34 } 35 } 36 return dp[n][m][0]; 37 } 38 39 int main() { 40 scanf("%d", &T); 41 for(int t = 1; t <= T; ++t) { 42 scanf("%d%d", &n, &m); 43 for(int i = 1; i <= n; ++i) 44 for(int j = 1; j <= m; ++j) scanf("%d", &mat[i][j]); 45 printf("Case %d: There are %I64d ways to eat the trees.\n", t, solve()); 46 } 47 }
代码(0MS)(hash)(下面代码是lld的……):


1 #include <iostream> 2 #include <algorithm> 3 #include <cstring> 4 #include <cstdio> 5 using namespace std; 6 typedef long long LL; 7 8 const int MAXH = 20010; 9 const int SIZEH = 13131; 10 11 struct hash_map { 12 int head[SIZEH]; 13 int next[MAXH], state[MAXH]; 14 LL val[MAXH]; 15 int size; 16 17 void init() { 18 memset(head, -1, sizeof(head)); 19 size = 0; 20 } 21 22 void insert(int st, LL sv) { 23 int h = st % SIZEH; 24 for(int p = head[h]; ~p; p = next[p]) { 25 if(state[p] == st) { 26 val[p] += sv; 27 return ; 28 } 29 } 30 state[size] = st; val[size] = sv; next[size] = head[h]; head[h] = size++; 31 } 32 } hashmap[2]; 33 34 int getB(int state, int i) { 35 return (state >> i) & 1; 36 } 37 38 void setB(int &state, int i, int val) { 39 state = (state & ~(1 << i)) | (val << i); 40 } 41 42 int mat[14][14]; 43 int n, m, T; 44 hash_map *cur, *last; 45 46 void update(int state, LL val, int x, int y) { 47 int left = getB(state, y); 48 int up = getB(state, y + 1); 49 if(mat[x][y] == 0) { 50 if(left == 0 && up == 0) cur->insert(state, val); 51 return ; 52 } 53 if(left == 0 && up == 0) { 54 if(x < n - 1 && y < m - 1) { 55 int newState = state; 56 setB(newState, y, 1); 57 setB(newState, y + 1, 1); 58 cur->insert(newState, val); 59 } 60 } else if(left == 0 || up == 0) { 61 if(x < n - 1) { 62 int newState = state; 63 setB(newState, y, 1); 64 setB(newState, y + 1, 0); 65 cur->insert(newState, val); 66 } 67 if(y < m - 1) { 68 int newState = state; 69 setB(newState, y, 0); 70 setB(newState, y + 1, 1); 71 cur->insert(newState, val); 72 } 73 } else { 74 int newState = state; 75 setB(newState, y, 0); 76 setB(newState, y + 1, 0); 77 cur->insert(newState, val); 78 } 79 } 80 81 LL solve() { 82 cur = hashmap, last = hashmap + 1; 83 last->init(); 84 last->insert(0, 1); 85 for(int i = 0; i < n; ++i) { 86 int sz = last->size; 87 for(int k = 0; k < sz; ++k) last->state[k] <<= 1; 88 for(int j = 0; j < m; ++j) { 89 cur->init(); 90 sz = last->size; 91 for(int k = 0; k < sz; ++k) 92 update(last->state[k], last->val[k], i, j); 93 swap(cur, last); 94 } 95 } 96 for(int k = 0; k < last->size; ++k) 97 if(last->state[k] == 0) return last->val[k]; 98 return 0; 99 } 100 101 int main() { 102 scanf("%d", &T); 103 for(int t = 1; t <= T; ++t) { 104 scanf("%d%d", &n, &m); 105 for(int i = 0; i < n; ++i) 106 for(int j = 0; j < m; ++j) scanf("%d", &mat[i][j]); 107 printf("Case %d: There are %lld ways to eat the trees.\n", t, solve()); 108 } 109 }




 本文探讨了DotA游戏中一个有趣的数学问题——如何利用回路覆盖矩阵上的树木。通过插头动态规划的方法解决了该问题,并提供了两种实现方案,一种是普通推法,另一种则采用了哈希表优化。
本文探讨了DotA游戏中一个有趣的数学问题——如何利用回路覆盖矩阵上的树木。通过插头动态规划的方法解决了该问题,并提供了两种实现方案,一种是普通推法,另一种则采用了哈希表优化。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








