数学：整数拆分-带约束

最新推荐文章于 2025-08-18 07:00:00 发布

weixin_30419799

最新推荐文章于 2025-08-18 07:00:00 发布

阅读量187

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/aininot260/p/9492162.html

本文介绍了一道整数拆分问题HDU4658的解法，利用五边形数定理和母函数理论，探讨了如何在限制条件下求解整数拆分的方法。

HDU4658：使用五边形数定理和母函数进行约束整数拆分

之前的那个一个题的公式是这样的：

f[n]=∑(-1)^(k-1)*(f[n-k*(3*k-1)/2]+f[n-k*(3*k+1)/2])

其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0；

加入了限制条件：拆分出来的整数中，任意整数都不能出现k次或k次以上

因此求的时候要使用公式的推导定理，母函数来求

生成函数（也有叫做“母函数”的）是说，构造这么一个多项式函数g(x)，使得x的n次方系数为f(n)

1+x+x^2+...

其中的系数f[n]就是全由1组成的n有多少种

1+x^2+x^4+...

其中的系数f[n]就是全由2组成的n有多少种

把这两个式子乘起来就变成了

(1+x+x^2..;.)*(1+x^2...)=1+x+2*x^2+x^3+x^4...

其中x^2系数2表示拆分整数2的方案数

无限制的拆分就可以理解成

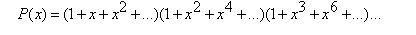中x^n的系数就是所求值

这题加了k的限制，所以得到的生成函数式

G(x)=(1+x+x^2+...+x^(k-1))*(1+x^2+x^4+x^2(k-1))*...

=(1-x^k)/(1-x)*(1-x^2k)/(1-x^2)*(1-x^3k)/(1-x^3)...

令y=x^k

=∏(1-y^i)/∏(1-x^i)（1<=i<∞）

=Q(x^k)/Q(x) (根据五边形数定理得)

=Q(x^k)*P(x)

∏(1-x^i)形式的可用五边形数定理来求

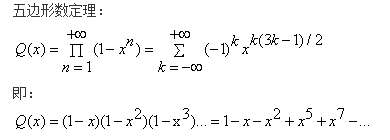
然后用这个公式代入

=Q(x^k)*P(x)
=( 1 - x^k - (x^k)^2 + (x^k)^5 + (x^k)^7 -... ) * ( 1 + x + 2*x^2 + 3*x^3 + 5*x^4 + 7*x^5 + ... )

这里的P（x）就是无限制拆分里面的那个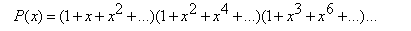

它的计算方法是：

p[n]=∑(-1)^(k-1)*(p[n-k*(3*k-1)/2]+p[n-k*(3*k+1)/2])

这样只需要求(1-x^k-x^2k+x^5k+x^7k-x^12k-x^15k+x^22k+x^26k)*(1+p(1)x+p(2)x+p(3)x+...)中x^n的系数了

 1 #include<cstdio>
 2 using namespace std;
 3 const int MOD=1e9+7;
 4 int n,k;
 5 int dp[100005];
 6 void init()
 7 {
 8     dp[0]=1;
 9     for(int i=1;i<=100000;i++)
10     {
11         for(int j=1,r=1;i-(3*j*j-j)/2>=0;j++,r*=-1)
12         {
13             dp[i]+=dp[i-(3*j*j-j)/2]*r;
14             dp[i]%=MOD;
15             dp[i]=(dp[i]+MOD)%MOD;
16             if(i-(3*j*j+j)/2>=0)
17             {
18                 dp[i]+=dp[i-(3*j*j+j)/2]*r;
19                 dp[i]%=MOD;
20                 dp[i]=(dp[i]+MOD)%MOD;
21             }
22         }
23     }
24 }
25 int solve(int n,int k)
26 {
27     int ans=dp[n];
28     for(int j=1,r=-1;n-k*(3*j*j-j)/2>=0;j++,r*=-1)
29     {
30         ans+=dp[n-k*(3*j*j-j)/2]*r;
31         ans%=MOD;
32         ans=(ans+MOD)%MOD;
33         if(n-k*(3*j*j+j)/2>=0)
34         {
35             ans+=dp[n-k*(3*j*j+j)/2]*r;
36             ans%=MOD;
37             ans=(ans+MOD)%MOD;
38         }
39     }
40     return ans;
41 }
42 int main()
43 {
44     init();
45     int T;
46     scanf("%d",&T);
47     while(T--)
48     {
49         scanf("%d%d",&n,&k);
50         printf("%d\n",solve(n,k));
51     }
52     return 0;
53 }