工作分配问题与算法优化-优快云博客

本文探讨了工作分配问题，即在不同人员执行不同任务时，如何通过算法设计实现总成本最小化。介绍了基本的解空间图例和限制函数概念，分享了一段C++代码实现，并讨论了算法中的剪枝技巧及时间复杂度问题。

1. 题目

2. 问题描述：工作分配问题，每个人做不同的工作需要支付不同的费用，需要设计算法合理地分配工作使总费用最小。

3. 基本的解空间图例：

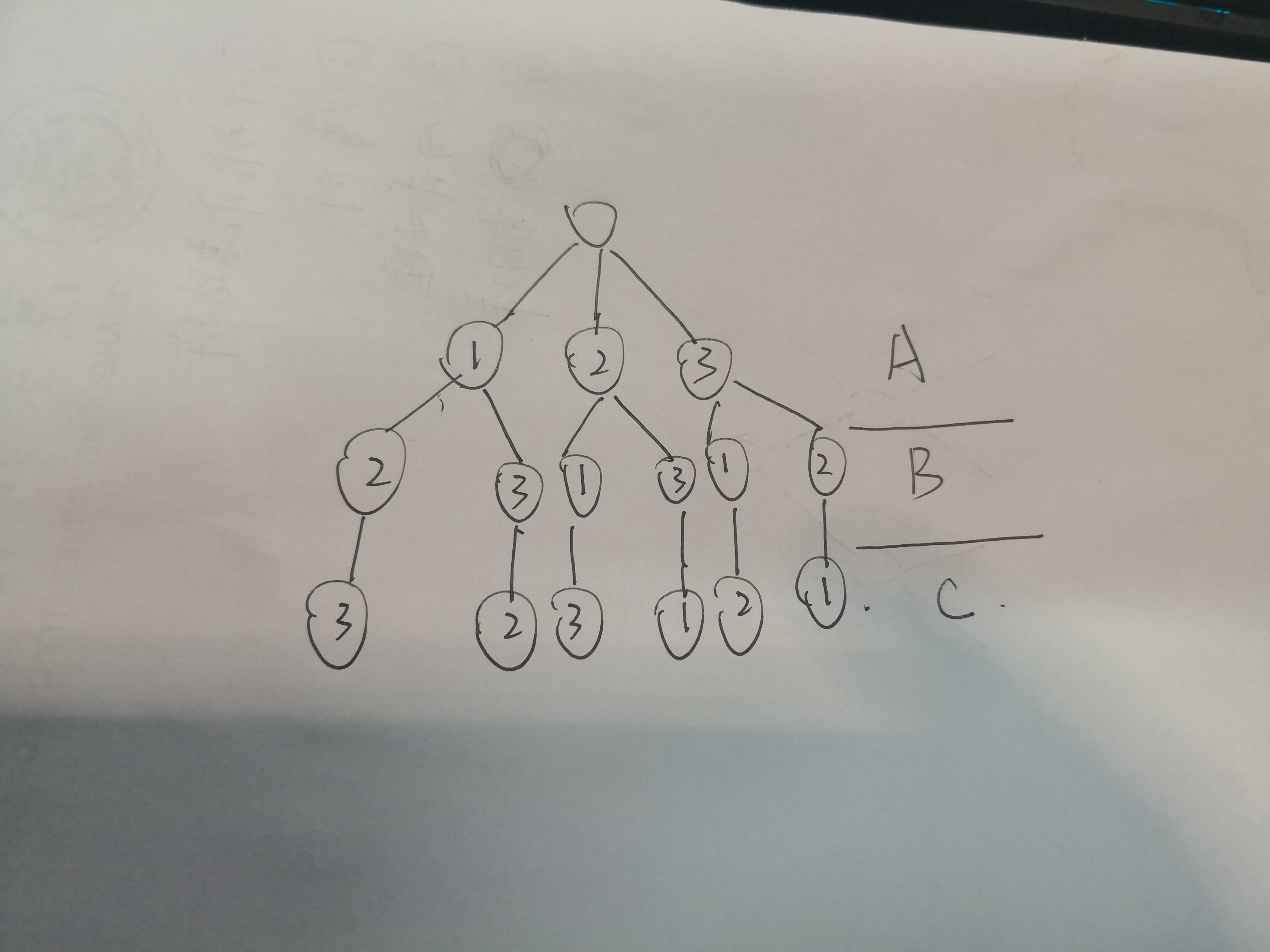
限制函数保证最后的解一定是最小值。

4. 代码：

#include<iostream>
using namespace std;
#define MAX 1000
int n;
int w[21][21];
int cp;//積累的工作費用
int bestp=MAX;//最少工作費用
int x[21];//當前路徑
int best[21];//最少工作費用的路徑
void swap(int a,int b)
{
        int temp=x[a];
        x[a]=x[b];
        x[b]=temp;
}
void backtrack(int i)
{
        if(i>n)
        {
                //限界函數保證了一定小於bestp 
                        bestp=cp;
                        for(int j=1;j<=n;j++)
                        best[j]=x[j];

                return;
        }
        else for(int j=i;j<=n;j++)
        {
                if(cp+w[i][x[j]]<bestp)
                {
                        cp+=w[i][x[j]];
                        swap(i,j);
                        backtrack(i+1);
                        swap(i,j);
                        cp-=w[i][x[j]];
                }
        }
} 

int main()
{
        cin>>n;
        for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                        cin>>w[i][j];
        for(int i=1;i<=n;i++)
        x[i]=i;
        cp=0;
        backtrack(1);
        cout<<bestp; 
        return 0;
}