分治与蛮力算法实践-优快云博客

本文介绍了一种通过分治法实现的快速排序算法及其调试过程，同时展示了利用蛮力法实现的冒泡排序算法。通过对两种算法的对比，帮助读者理解其基本原理和应用场景。

实验说明

实验名称：蛮力与分治算法应用

实验课程：一

所属院系：计数院软件工程

所属课程：算法设计与分析

课程目的：

蛮力法就是主要是一种简单直接解决问题的方法，例如：顺序和穷举查找、字符匹配、选择和冒泡排序等，分治法主要是将复杂的问题分解成一系列较小的问题，然后合并这些小问题的解。

实验要求:

应用蛮力法和分治策略设计问题求解算法，并编写程序，解决实际问题。本实验就是应用蛮力法和分治法，设计并实现选择排序，合并排序，或快速排序程序。
要求学生能理解蛮力法和分治法的基本原理，解决实际问题，实现上述应用程序。并给出足够的测试实例，分析实验结果，并证明算法的正确性。

实验内容

分治算法
分治算法是一个很著名的算法。将一个问题一分为二，再从两份中去分。从而减少运算的次数，也提高了算法的效率。
（1）将一个问题划分为多个子问题：子问题规模最好相同；
（2）对这些子问题的问题求解，一般使用递归的方法，当然问题规模很小的时候也可以用另外的算法；
（3）在问题需要的时候合并子问题的解，从而得到原始问题的答案；

实验代码

#include<stdio.h>
typedef int Elemtype ;
#define MAN 10
void operation(Elemtype *T);
void swap(Elemtype *T,int i,int j){
    int tum;
    tum = T[i];
    T[i] = T[j];
    T[j] = tum;
}
int HoarePartition(Elemtype *T,int l,int r){
    int i=l,j=r;
    int p = T[l];
    while(j>i){
        for(;i<=r;i++){
            if(T[i]>p)break;
        }
        for(;j>l;j--){
            //printf("qqqqff%d,%d,i:%d ",j,T[j],i);
            if (T[j]<p)break; 
        }
        swap(T,i,j);
    }
    swap(T,i,j);
    swap(T,l,j);
    return j;
    
}
void Getlevel(Elemtype *T,int l,int r){
    if((r-l)<=1){
        return;
    }
    int level;
    operation(T);//getchar();
    level = HoarePartition(T,l,r);
    //printf("j=%d;T[j]=%d,l=%d,r=%d",level,T[level],l,r);
    //getchar();
    Getlevel(T,l,level);
    Getlevel(T,level+1,r);
    
}
void operation(Elemtype *T){
    int i= 0;
    for(i= 0;i<10;i++){
        printf("%d ",T[i]);
        }
    //printf("%d,",T[10]);
    printf("i=%d\n",--i);
}
int main(){
    int T[MAN] = {5,11,2,6,8,9,4,22,14,7};
    operation(T);
    Getlevel(T,0,MAN-1);
    operation(T);
    return 0;
}

实验结果及调试过程：
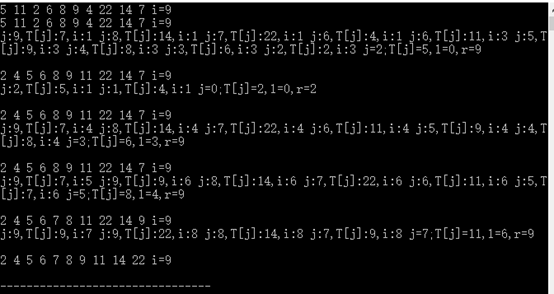
测试数组为：int T[MAN] = {5,11,2,6,8,9,4,22,14,7};
下面为每次递归的步骤过程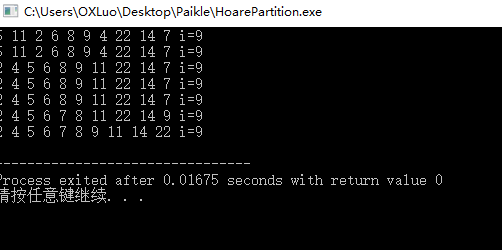

蛮力算法：简单直接

程序代码：

#include<stdio.h>
//冒泡排序 
void swap(int *T,int l){
    int t;
    t = T[l] ;
    T[l] = T[l+1];
    T[l+1] = t;
}
void operation(int T[]){
    for(int i = 0;i<10;i++)
        printf("%d ",T[i]);
}
int main(){
    int T[] = {1,5,6,8,2,11,66,4,2,9};
    
    for(int i=0;i<10;i++)
        for(int j=0;j<9-i;j++){
            if(T[j]>T[j+1]){
                swap(T,j);
            }
        }
    operation(T); 
    return 0 ;
}

测试数据：int T[] = {1,5,6,8,2,11,66,4,2,9};
实验结果：