动态规划题型总结

还有不到一个月就要比noip了，鉴于动态规划是很重要的一个考点，我决定在此做一个小总结。

一、背包问题

背包问题是最基础的动态规划，基本问题（也就是01背包问题）是：一个背包总容量为V，现在有N个物品，第i个 物品体积为weight[i]，价值为value[i]，现在往背包里面装东西，怎么装能使背包的内物品价值最大？

这道题的思路是，建立一个数组f[i],用来储存体积为i时价值的最大值。然后用一个双重循环就解决了。

下面是一道01背包的裸题：装箱问题

题目描述

有一个箱子容量为V（正整数，0＜＝V＜＝20000），同时有n个物品（0＜n＜＝30，每个物品有一个体积（正整数）。

要求n个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入输出格式

输入格式：
一个整数，表示箱子容量

 一个整数，表示有n个物品

 接下来n行，分别表示这n 个物品的各自体积

 输出格式：
一个整数，表示箱子剩余空间。

输入输出样例

输入样例#1：

24 6 8 3 12 7 9 7

输出样例#1：

0

说明

NOIp2001普及组 第4题

代码：

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 using namespace std;
 8 int v[35];
 9 int f[20101];
10 int main()
11 {
12     int V,n;
13     scanf("%d%d",&V,&n);
14     for(int i=1;i<=n;i++) scanf("%d",&v[i]);
15     for(int i=1;i<=n;i++)
16     {
17         for(int j=V;j>=v[i];j--)
18         {
19             f[j]=max(f[j],f[j-v[i]]+v[i]);
20         }
21     }
22     printf("%d",V-f[V]);
23     return 0;
24 }

zxwt

下面是稍微复杂一点的：开心的金明

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的N元。于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是整数元）。他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，……，jk，则所求的总和为：

v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。（其中*为乘号）

请你帮助金明设计一个满足要求的购物单。

输入输出格式

输入格式：

 

输入的第1行，为两个正整数，用一个空格隔开：

N m （其中N（<30000）表示总钱数，m（<25）为希望购买物品的个数。）

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有2个非负整数

v p （其中v表示该物品的价格(v<=10000)，p表示该物品的重要度(1~5)）

 

输出格式：

 

输出只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<100000000）。

 

输入输出样例

输入样例#1：

1000 5
800 2
400 5
300 5
400 3
200 2

输出样例#1：

3900

说明

NOIP 2006 普及组 第二题

这道题和上面的装箱问题唯一的不同就是，装箱的限制（箱子体积V）和目标（最少剩余体积）是一个东西，二这道题的限制（钱数N）和目标（乘积最大）不是一个东西。不过没关系，只要改变f数组里存的内容就好了。

代码:

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 using namespace std;
 8 struct data
 9 {
10     int v,p;
11 }a[30];
12 int f[30303];
13 int main()
14 {
15     int N,m;
16     scanf("%d%d",&N,&m);
17     for(int i=1;i<=m;i++) scanf("%d%d",&a[i].v,&a[i].p);
18     for(int i=1;i<=m;i++)
19     {
20         int tmp=a[i].v*a[i].p;
21         for(int j=N;j>=a[i].v;j--)
22         {
23             f[j]=max(f[j],f[j-a[i].v]+tmp);
24         }
25     }
26     printf("%d",f[N]);
27     system("pause");
28     return 0;
29 }

kxdjm

 

二、划分型dp

• 简介：简单来说就是需要把一个东西划分为m份，考虑如何划分最优。
• 例题：

1.noip2000 乘积最大

题目描述  Description                   

今年是国际数学联盟确定的“2000——世界数学年”，又恰逢我国著名数学家华罗庚先生诞辰90周年。在华罗庚先生的家乡江苏金坛，组织了一场别开生面的数学智力竞赛的活动，你的一个好朋友XZ也有幸得以参加。活动中，主持人给所有参加活动的选手出了这样一道题目：

 

设有一个长度为N的数字串，要求选手使用K个乘号将它分成K+1个部分，找出一种分法，使得这K+1个部分的乘积能够为最大。

 

同时，为了帮助选手能够正确理解题意，主持人还举了如下的一个例子：

 

有一个数字串：312， 当N=3，K=1时会有以下两种分法：

 

1)  3*12=36

2)  31*2=62

  

   这时，符合题目要求的结果是：31*2=62

 

   现在，请你帮助你的好朋友XZ设计一个程序，求得正确的答案。

输入描述  Input Description              

   程序的输入共有两行：

   第一行共有2个自然数N，K（6≤N≤40，1≤K≤6）

   第二行是一个长度为N的数字串。

 输出描述  Output Description              

   结果显示在屏幕上，相对于输入，应输出所求得的最大乘积（一个自然数）。

样例输入   Sample Input              

4  2

1231

样例输出  Sample Output              

62

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 using namespace std;
 8 long long t[50][50];
 9 long long s[50];
10 long long dp[50][10];
11 int main()
12 {
13     int n,k;
14     scanf("%d%d",&n,&k);
15     long long x;  //long long在这种解法中十分重要！
16     scanf("%lld",&x);
17     for(int i=n;i>=1;i--)
18     {
19         s[i]=x%10;
20         t[i][i]=s[i];
21         x/=10;
22     }
23     for(int i=1;i<n;i++)  //初始化：t[i][j]指从 i到 j的数 
24     {
25         for(int j=i+1;j<=n;j++)
26         {
27             t[i][j]=t[i][j-1]*10+s[j];
28             //cout<<t[i][j]<<" ";
29         }
30         //cout<<endl;
31     }
32     for(int i=1;i<=n;i++) dp[i][0]=t[1][i];   //初始化：dp[i][j]即为前 i个数字里添加 j个乘号的最大值 
33     
34     for(int i=1;i<=k;i++)
35         for(int j=i+1;j<=n;j++)
36             for(int h=i;h<j;h++)   //i,j中间的空当部分可以任意添加乘号 
37                 dp[j][i]=max(dp[j][i],dp[h][i-1]*t[h+1][j]);
38     printf("%d",dp[n][k]);
39     return 0;
40 }

codevs 1017

 2.noip2001 数的划分

题目描述 Description                   

将整数n分成k份，且每份不能为空，任意两种划分方案不能相同(不考虑顺序)。 例如：n=7，k=3，下面三种划分方案被认为是相同的。 1 1 5

1 5 1

5 1 1 问有多少种不同的分法。

 

 输入描述 Input Description              

输入：n，k (6<n<=200，2<=k<=6)

输出描述 Output Description              

输出：一个整数，即不同的分法。

 

样例输入 Sample Input              

 7 3

样例输出 Sample Output              

4

数据范围及提示 Data Size & Hint              

 {四种分法为：1，1，5;1，2，4;1，3，3;2，2，3;}

思路：dp[i][j]指前i个数被划分为j份。

有两种情况：1）可以划分出一个1：前提是后面可以继续分下去，即有解。这是可以减少一个j，即dp[i-1][j-1];

          2）无法划分出一个1：那么此时被划分出来的所有数中都没有1.前提是无法再分出1，因此要在每部分中都减去一个1，即dp[i-j][j];

因此转移方程为：dp[i][j]=dp[i-1][j-1]+dp[i-j][j];

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 using namespace std;
 8 int dp[210][10];
 9 int main()
10 {
11     int n,k;
12     scanf("%d%d",&n,&k);
13     dp[0][0]=1;  //应对i=j=1 
14     for(int i=0;i<=n;i++)
15         for(int j=1;j<=min(i,k);j++)
16             dp[i][j]=dp[i-1][j-1]+dp[i-j][j];
17     printf("%d",dp[n][k]);
18     //system("pause");
19     return 0;
20 }

codevs 1039

 

 

 三、区间型dp

• 简介：指一段区间上的dp，通过枚举左右子区间来求解。也就是说，先求出每一小段的最优解，之后合并成大区间的最优解。
• 例题：

石子归并

题目描述   Description                   

有n堆石子排成一列，每堆石子有一个重量w[i], 每次合并可以合并相邻的两堆石子，一次合并的代价为两堆石子的重量和w[i]+w[i+1]。问安排怎样的合并顺序，能够使得总合并代价达到最小。

 

输入描述   Input Description              

第一行一个整数n（n<=100）

第二行n个整数w1,w2...wn  (wi <= 100)

 

输出描述  Output Description              

一个整数表示最小合并代价

 

样例输入   Sample Input              

4

4 1 1 4

 

样例输出   Sample Output              

18

思路：

	1	2	3	4
1	4	/	/	/
2	5	1	/	/
3	8	2	1	/
4	18	8	5	4

上表是以样例为例，算出的i~j的最优解。

 

 1 #include <iostream>
 2 #include <cmath>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cstdlib>
 6 #include <algorithm>
 7 #define INF 2147483647
 8 using namespace std;
 9 int a[110];
10 int f[110][110];
11 int main()
12 {
13     int n;
14     scanf("%d",&n);
15     for(int i=1;i<=n;i++)
16     {
17         int x;
18         scanf("%d",&x);
19         a[i]=a[i-1]+x;   //前缀和 
20         f[i][i]=0;
21     }
22     for(int i=2;i<=n;i++)
23         for(int j=i-1;j>=1;j--)   //注意此处要从大到小，画图可知，是先知道大的再知道小的 
24         {
25             f[j][i]=INF;
26             for(int k=j;k<i;k++)   //把两个小区间合并 
27                 f[j][i]=min(f[j][i],f[j][k]+f[k+1][i]+a[i]-a[j-1]);
28         }
29     printf("%d",f[1][n]);
30     //system("pause");
31     return 0;
32 }

codevs 1048

 

四、序列型dp

•  简介：没有找到对于这种dp的准确定义，但是根据自己的理解，大概意思就是在一个序列上dp，dp过程中需要借助这个序列的一些特殊性（比如无法交换顺序或者序列的覆盖、重叠性等等）。
• 例题：

1.最长上升子序列

 

题目描述 Description

给一个数组a1, a2 ... an，找到最长的上升降子序列ab1<ab2< .. <abk，其中b1<b2<..bk。

输出长度即可。

 

输入描述 Input Description

第一行，一个整数N。

第二行 ，N个整数（N < = 5000）

 

输出描述 Output Description

输出K的极大值，即最长不下降子序列的长度

 

样例输入 Sample Input

5

9 3 6 2 7

 

样例输出 Sample Output

3

 

数据范围及提示 Data Size & Hint

【样例解释】

最长不下降子序列为3,6,7

思路：这差不多是最简单的dp了，很轻易就能想到，用dp[i]表示前i个数的最长上升子序列。那么只要从i之前找到比a[i]小的数，在那个数列个数的基础上+1即可。

（代码暂略）

2.线段覆盖

 

题目描述 Description

    给定x轴上的N（0<N<100）条线段，每个线段由它的二个端点a_I和b_I确定，I=1,2,……N.这些坐标都是区间（－999，999）的整数。有些线段之间会相互交叠或覆盖。请你编写一个程序，从给出的线段中去掉尽量少的线段，使得剩下的线段两两之间没有内部公共点。所谓的内部公共点是指一个点同时属于两条线段且至少在其中一条线段的内部（即除去端点的部分）。

 

输入描述 Input Description

    输入第一行是一个整数N。接下来有N行，每行有二个空格隔开的整数，表示一条线段的二个端点的坐标。

 

输出描述 Output Description

    输出第一行是一个整数表示最多剩下的线段数。

 

样例输入 Sample Input

3

6  3

1  3

2  5

 

样例输出 Sample Output

2

 

数据范围及提示 Data Size & Hint

0<N<100

 

 思路：按右端点从小到大排序，之后只需要判断当前的左端点是否在上一个未删除的数的右端点的左边就行了。注意不能按照左端点排序，理由如下：

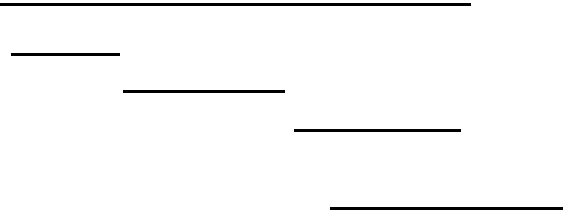如图这种情况，会把中间三条边删掉，而不是删第一条边；因此不是最优解。

转载于:https://www.cnblogs.com/lulala/p/7688969.html