LeetCode第235题 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

 

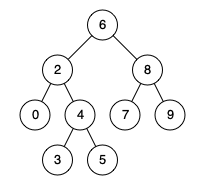
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

思路: 二叉树的基本性质: 左孩子.val<root.val<右孩子.val
      对于输入的p和q,并没有严格给出那个是左孩子那个是右孩子.
      1.如果 root.val大于等于其中一个,并且小于等于另一个.说明 p,q一个在root左边一个在root右边  return;
      2.假设p为左孩子,q为右孩子. 那么使  情况1不满足并且能让右孩子成为root的情况是:   (p本应该在root左边,却不在 &&  p 老老实实在root右边)
          即 root.val < p.val && root < q.val
      3.好了,既然情况1不满足,并且搜索右孩子的情况也不满足,直接以左孩子为root搜索.


        注意第二步是假设p为左孩子,q为右孩子 , 那么 如果假设不成立,即p为右孩子,q为左孩子为什么不会出错呢?
        由于题目没有给出严格的左右孩子限制,而你又不想swap(p,q)以保证谁是左孩子谁是右孩子,就必须考虑这个问题.

        答案肯定是不会出错 : 如果 p为右孩子,q为左孩子
            那么能让右孩子成为root的情况是: root.val < p.val && root < q.val , 是的,与第二步相同.
            p.val与q.val的大小关系没有成为阻碍.不管孰大孰小,return 的终止条件是通过情况1判断的.

 1 class Solution235 {
 2 
 3   public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
 4     if ((root.val - p.val) * (root.val - q.val) <= 0) { //异号
 5       return root;
 6     }
 7     if (p.val > root.val && root.val < q.val) {
 8       return lowestCommonAncestor(root.right, p, q);
 9     }
10     return lowestCommonAncestor(root.left, p, q);
11   }
12 }

 

转载于:https://www.cnblogs.com/rainbow-/p/10386663.html