玩Google 纵横

Google maps谷歌地图挺不错的，界面清新自然，操作起来也很简单，而且地图采用了数据实时更新下载，相比大部分的GPS导航软件动不动就几百MB的大地图，Google maps的体积很小，软件不到2MB，总是有种“绿色”的感觉，所以我一直都会在手机保留这个导航软件。

最近Google玩新花样，一个叫做“Google纵横”的功能，其实就是今年二月份流传的“Google Latitude”，目前已经有中文版本的Google地图支持这个功能了，我也在第一时间下载了3.0.0.12版试用。

以前Google地图只是单一的导航软件，现在Google地图成了“Google纵横”的平台，我们在这个地图平台上，可以通过“纵横”功能，和好朋友交流位置信息。既然有了身份的识别，自然就需要一个账号了，所以我依照“Google纵横”的提示，先上Google的官网注册一个Google帐户，这个账户就是以后我在地图上的身份了。

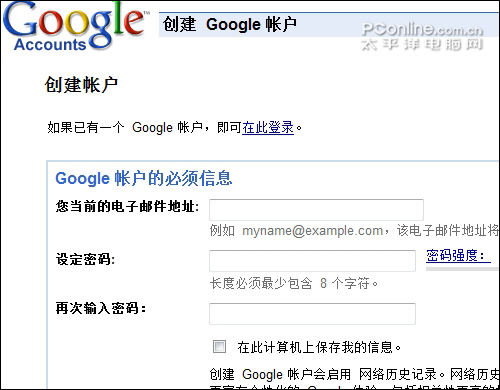
朋友Candy邀我明天陪她去买数码玩具，她的S60手机也安装了带Google纵横的Google地图，嘿嘿，我刚申请的Google账号派上用场了！我现在使用的机子的多普达的Touch HD，480*800分辨率的3.8英寸大屏幕，看地图十分轻松！

我打开Google地图，点击右下角的菜单，可以看到“加入纵横”功能，点一下，输入Google账户的用户名和密码，点一下登陆，就进入了我的好友列表，上面显示红色的“1个新的共享请求”，看来是Candy加我了。

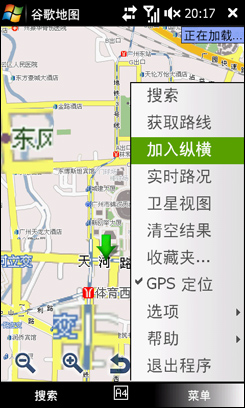
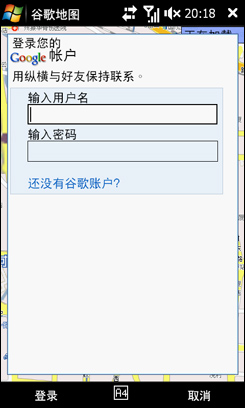
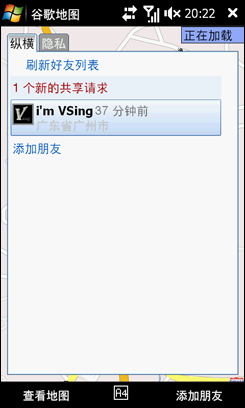
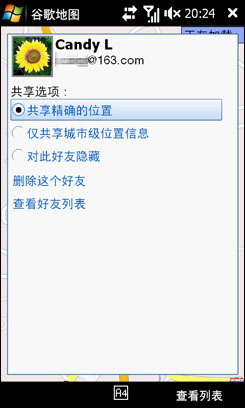
点一下，果然是Candy，这个时候可以设置我自己的状态，可以向他共享我现在的位置，也可以隐藏，就选接受吧。这是回到好友列表，就可以看到Candy了。

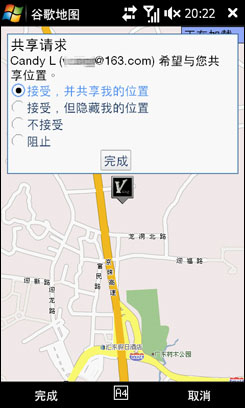
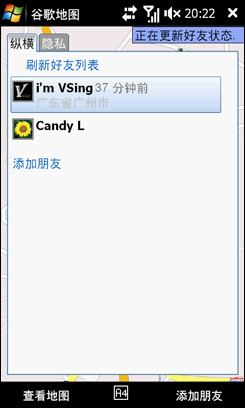
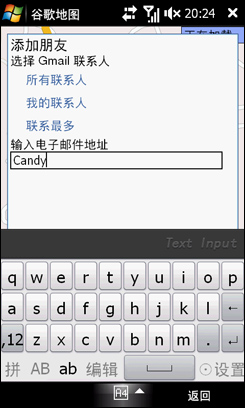
刚才是Candy加我，如果我要主动加朋友为好友，应该怎么操作？“添加好友”功能就在好友列表的下方嘛，点一下，输入对方的Google账号，其实就是对方的E-mail地址，然后设置是否公开自己的位置信息，就OK了。Google纵横还是延续了Google地图简单、易用的理念。

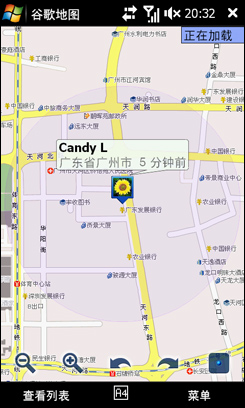
与Candy加为好友，第一时间看看她在哪里！可以看到Candy的向日葵头像在天河东路，我现在则在天河北路。

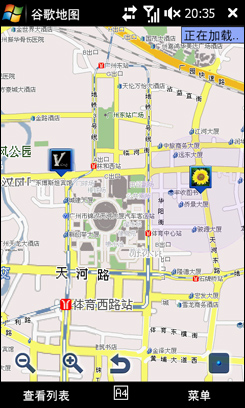
十五分钟以后……

Candy来电“hello，我已经到太平洋数码广场，我们会和吧”，嘿嘿，让我看看Google纵横准不准，打开一看，Candy果然到了，在石牌西路。让Google地图帮我规划路线吧，点一下“获取路线”，起点是我目前的位置，终点是Candy的位置。

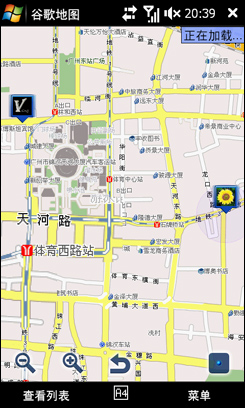
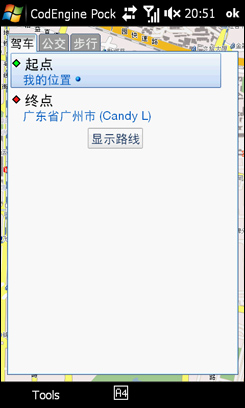
几秒钟，路线就规划好了，除了文字的表述，地图上有红色的线将线路表示出来。可以看到路线的终点就是石牌西路，太平洋数码广场！

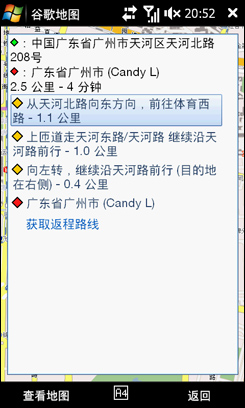
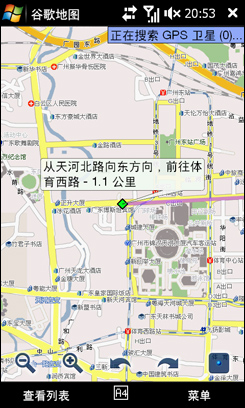
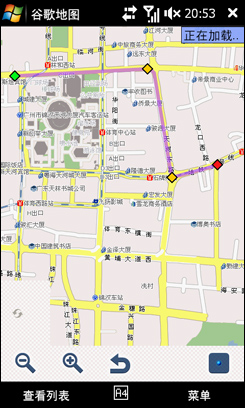
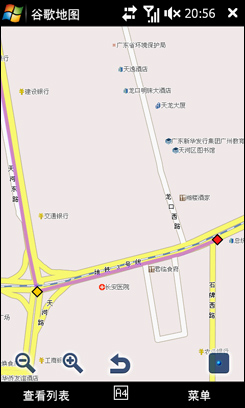
有了Google纵横的帮忙，出行与友人见面变得如此简单有趣。对于很多集体出行的活动，例如车友会出游等等，在车上打开Google纵横，就能够掌握大家目前的位置，不用担心有掉队的情况，能够实时更新友人的位置，这正是Google纵横最大的意义所在。

转载于:https://www.cnblogs.com/mmmhhhlll/archive/2010/03/29/1700104.html