有限差分估计梯度:
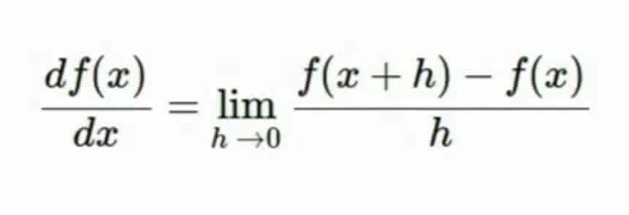
写起来简单,但速度慢而且结果区分度不大
解析梯度:
计算图:
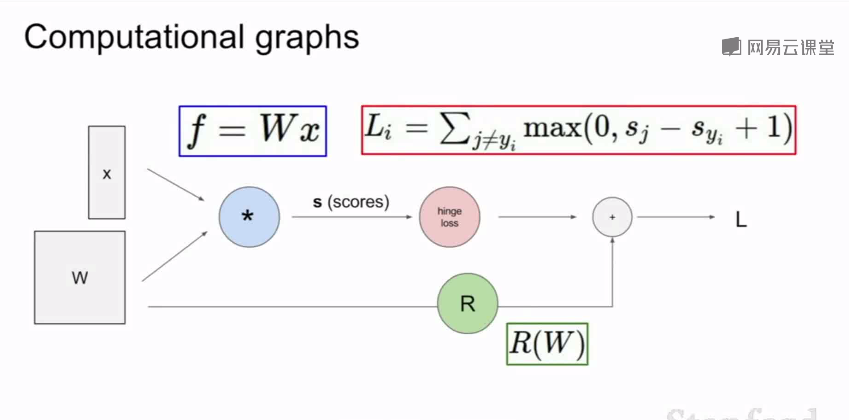
反向传播工作机制:
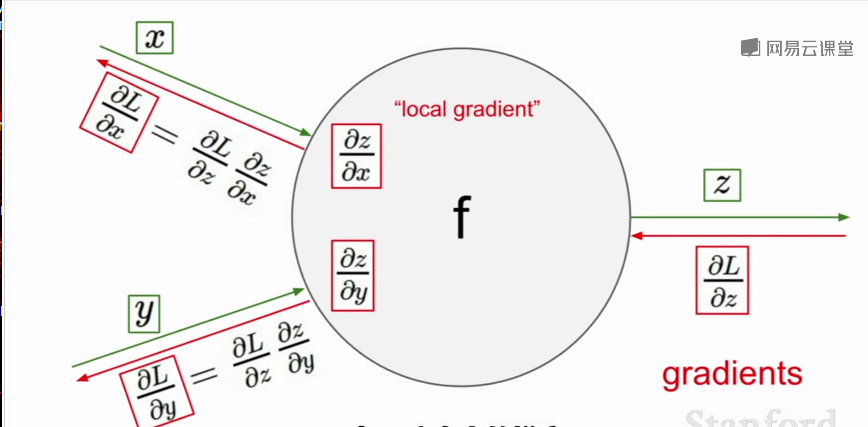
从输出开始乘以每个节点的本地梯度,一直传递到输入
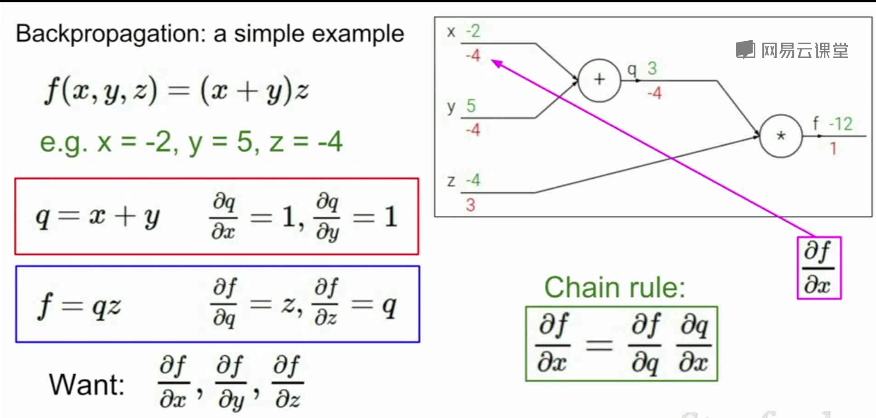
梯度从后向前传播(链式法则)

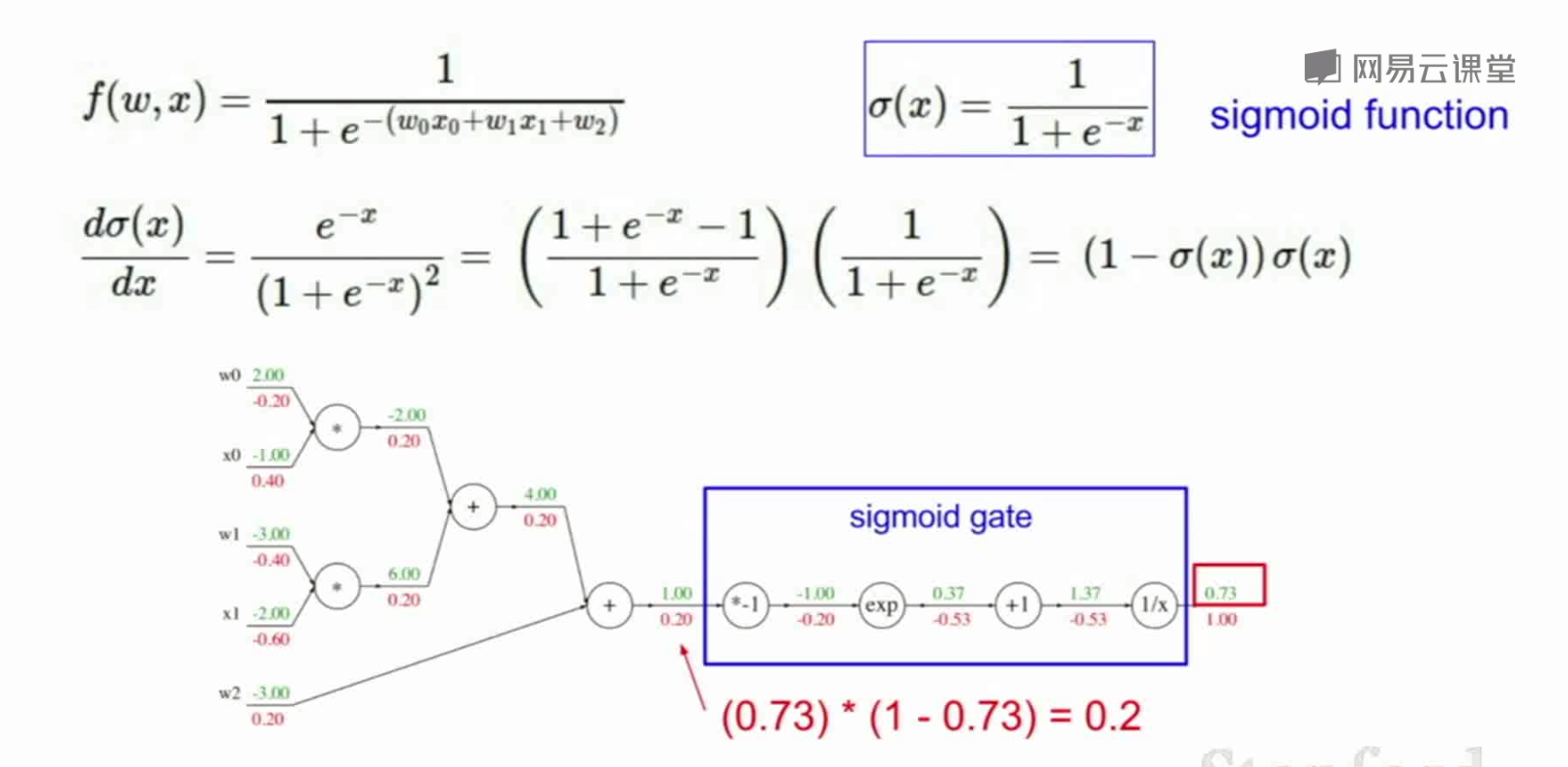
sigmoid函数:
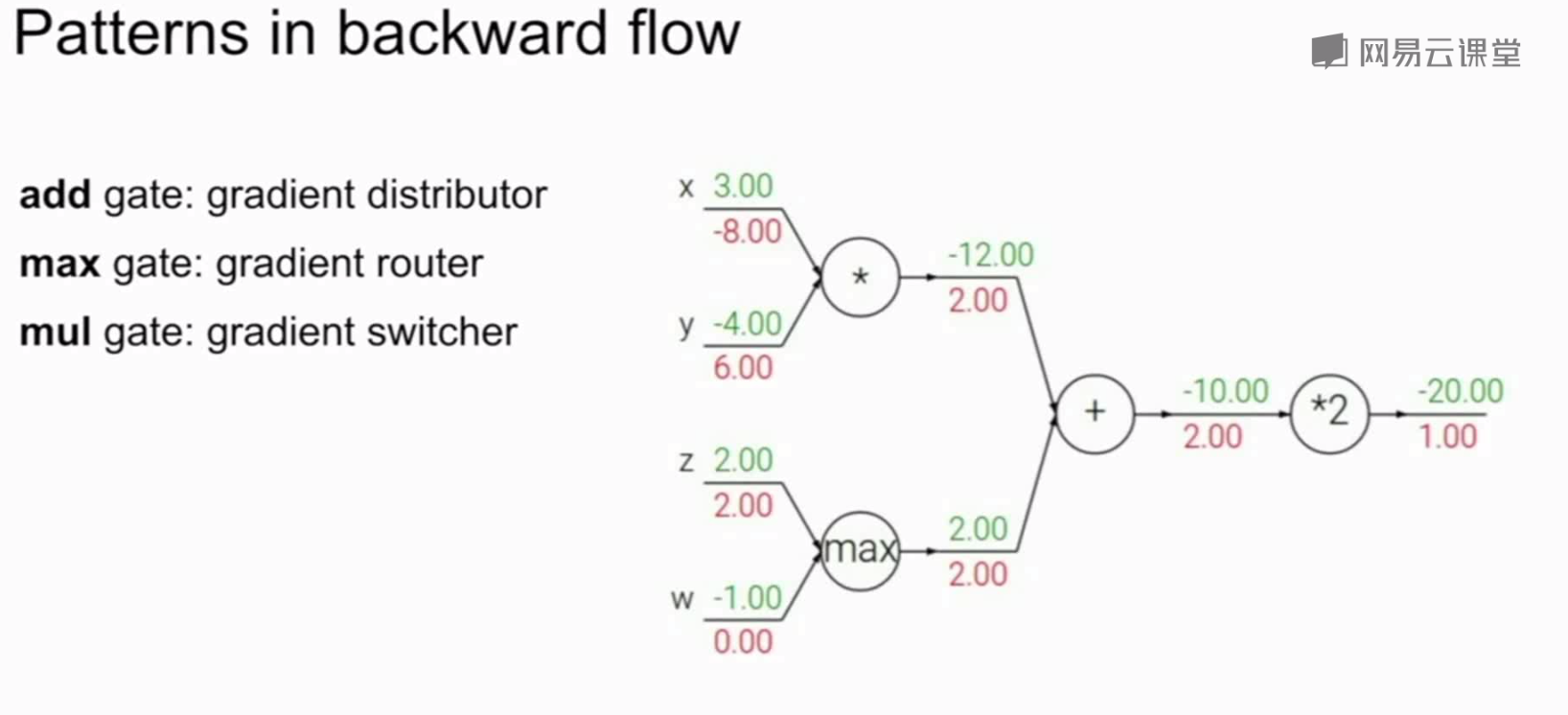
加法门、max门、乘法门:
加法门相当于分配梯度
max门相当于路由器,将梯度传给上游最大值所在节点
乘法门相当于转换器
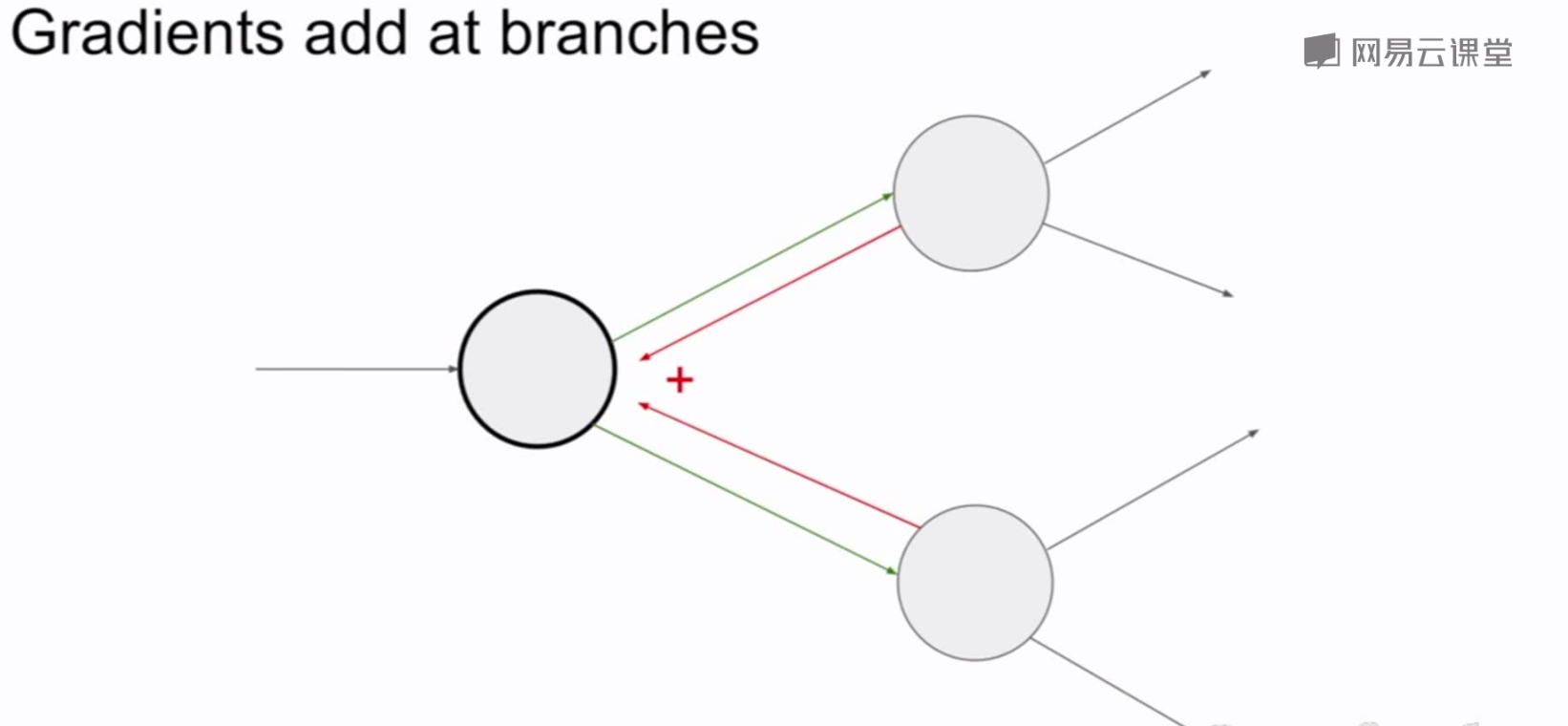
多个神经元在节点处相加的梯度等于每个神经元的梯度相加的和
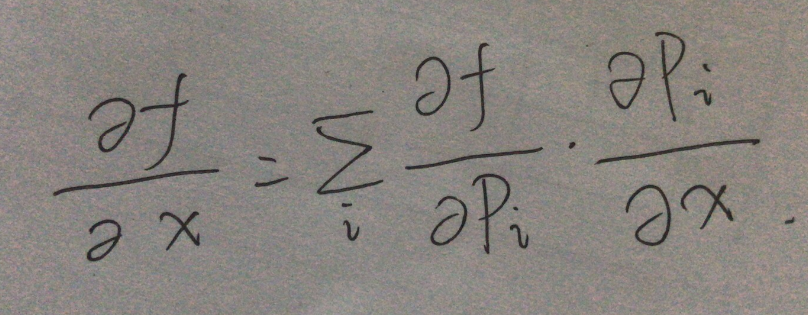
向量的反向传播:
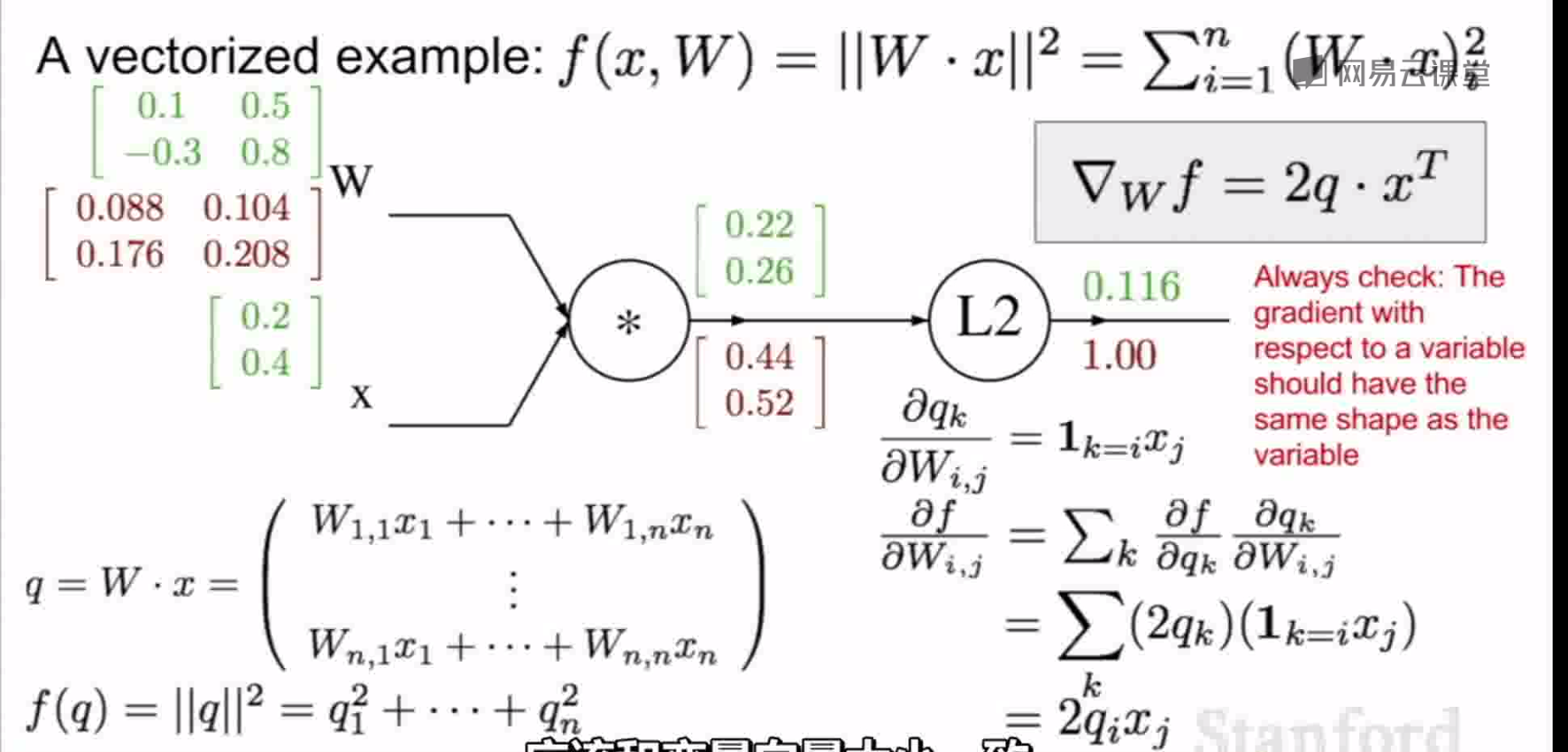
反向传播api:

例:

summary:

1
 深度学习反向传播原理
深度学习反向传播原理
 本文深入探讨了深度学习中反向传播的工作机制,包括有限差分估计梯度的局限性,解析梯度的计算图,以及反向传播如何通过链式法则从输出层向输入层传递梯度。同时,介绍了sigmoid函数及其在神经网络中的作用,以及加法门、max门和乘法门如何影响梯度的分配和转换。
本文深入探讨了深度学习中反向传播的工作机制,包括有限差分估计梯度的局限性,解析梯度的计算图,以及反向传播如何通过链式法则从输出层向输入层传递梯度。同时,介绍了sigmoid函数及其在神经网络中的作用,以及加法门、max门和乘法门如何影响梯度的分配和转换。
有限差分估计梯度:
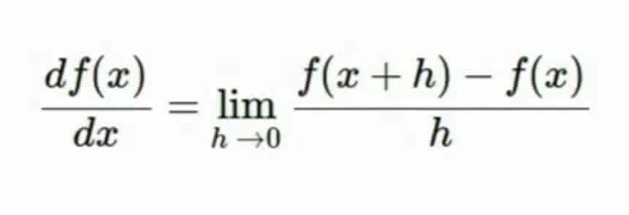
写起来简单,但速度慢而且结果区分度不大
解析梯度:
计算图:

反向传播工作机制:
从输出开始乘以每个节点的本地梯度,一直传递到输入

梯度从后向前传播(链式法则)


sigmoid函数:

加法门、max门、乘法门:
加法门相当于分配梯度
max门相当于路由器,将梯度传给上游最大值所在节点
乘法门相当于转换器

多个神经元在节点处相加的梯度等于每个神经元的梯度相加的和

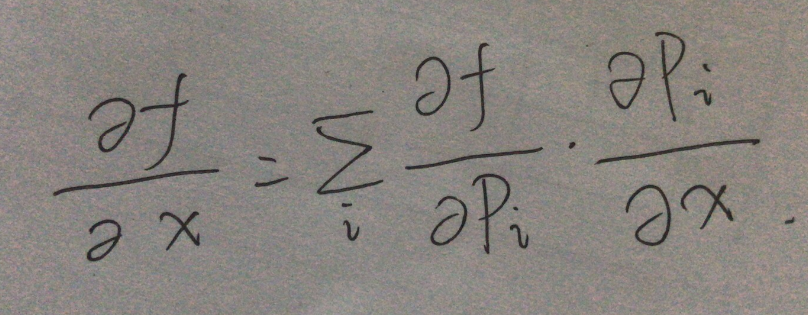
向量的反向传播:

反向传播api:

例:

summary:

1
转载于:https://www.cnblogs.com/Manuel/p/10994305.html

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


