最小生成树

最新推荐文章于 2023-07-25 20:08:11 发布

转载最新推荐文章于 2023-07-25 20:08:11 发布 · 102 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Kurokey/p/5725170.html

本文介绍了一种解决三维空间中点集构成最小生成树的问题。通过将各维度上坐标相近的点进行连接，利用优先队列实现Kruskal算法求解最小生成树。

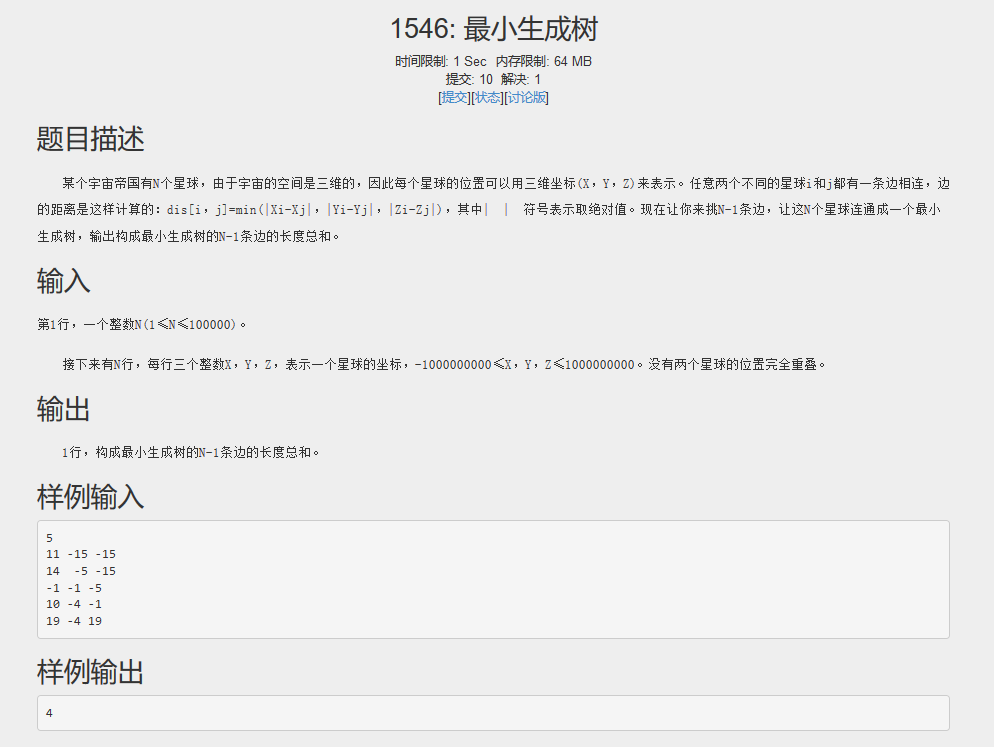
题目思路: 要充分利用距离计算公式，也就是说尽可能的把某一维度坐标上相近的点连接起来。

　　也就是说我们可以把每个点分三次情况考虑(因为只有三维)，把每一维度按从小到大排序，相邻两点间距离就是这两个点关于这一维度上的最小值。

　　　　我们把点对和距离用结构体保存放到优先队列去，按距离从小到大 Kruskal 求最小生成树即可。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <stack>
#include <cctype>
#include <queue>
#include <string>
#include <vector>
#include<functional>
#include <set>
#include <map>
#include <climits>
#define lson root<<1,l,mid
#define rson root<<1|1,mid+1,r
#define fi first
#define se second
#define ping(x,y) ((x-y)*(x-y))
#define mst(x,y) memset(x,y,sizeof(x))
#define mcp(x,y) memcpy(x,y,sizeof(y))
using namespace std;
#define gamma 0.5772156649015328606065120
#define MOD 1000000007
#define inf 0x3f3f3f3f
#define N 100005
#define maxn 10005
typedef pair<int,int> PII;
typedef long long LL;

int n,m,k,x,y,t1;
int fp[N],has[N];
int findp(int x){return fp[x]==x?x:fp[x]=findp(fp[x]);}
struct Node{
    int x,y,z,id;
    Node(){}Node(int a,int b,int c):x(a),y(b),z(c){}
}node[N];
struct Edge{
    int x,y,v;
    bool operator<(const Edge&a)const{
        return v>a.v;
    }
    Edge(){}
    Edge(int a,int b,int c):x(a),y(b),v(c){}
};
priority_queue<Edge>q;
bool cmp1(const Node&a,const Node&b){return a.x<b.x;}
bool cmp2(const Node&a,const Node&b){return a.y<b.y;}
bool cmp3(const Node&a,const Node&b){return a.z<b.z;}
void solve(){
    int cnt=1;
    LL ans=0;
    while(cnt<n){
        Edge temp=q.top();q.pop();
        x=findp(temp.x);
        y=findp(temp.y);
        if(x!=y){
            fp[x]=y;
            ans+=temp.v;
            ++cnt;
        }
    }
    printf("%lld\n",ans);
}
int main(){
    int i,j,group,x,y;
    scanf("%d",&n);
    for(i=1;i<=n;++i){
        fp[i]=i;node[i].id=i;
        scanf("%d%d%d",&node[i].x,&node[i].y,&node[i].z);
    }
    sort(node+1,node+n+1,cmp1);
    for(i=2;i<=n;++i){
        q.push(Edge(node[i-1].id,node[i].id,abs(node[i].x-node[i-1].x)));
    }
    sort(node+1,node+n+1,cmp2);
    for(i=2;i<=n;++i){
        q.push(Edge(node[i-1].id,node[i].id,abs(node[i].y-node[i-1].y)));
    }
    sort(node+1,node+n+1,cmp3);
    for(i=2;i<=n;++i){
        q.push(Edge(node[i-1].id,node[i].id,abs(node[i].z-node[i-1].z)));
    }
    solve();
    return 0;
}