题目:返回一个整数数组中最大子数组的和
额外要求:让数组手尾相连,构成一个环,允许a[n],a[0]...这种形式。同时返回最大子数组的位置
设计思想:将环断开,成为一条线,分析这条线上的最大子数组,找到最大子数组,便可以找到最大子数组的起点和终点,然后将终点看作起点,将起点看作终点,将线连成环,在进行寻找最大子数组(寻找时不算上起点和终点),最后将先后找到的两个最大子数组连在一起就形成了这个整数组环的最大子数组,然后将记录的起点和终点输出出来,返回最大子数组的位置。
出现的问题:无法输入更多的数,例如1000个
可能的解决方案:定义更大范围的整形数组,但我用了 long,long long ,usinged long,usinged long long都不行
代码:
//吕广浩 3/27
#include<iostream>
#define n 100
using namespace std;
void main()
{
int a[n], b[n][n];
int length, i, j, w = 0, p = 0, q = 0, temp, m;
cout << "输入随机整数" << endl;
for (length = 0;;)
{
cin >> a[length];
length++;
if (getchar() == '\n')
{
break;
}
}
cout << "这个数组的长度为:" << length << endl;
//求子数组
for (i = 0; i<length; i++)//两次循环,进行排除法,判断每个数所构成的最大子数组
{
m = i;
w = 0;
j = 0;
while (j <= length - 1)
{
w += a[m];
b[i][j] = w;
m++;
if (m>length - 1)
{
m = 0;
}
j++;
}
}
temp = b[0][0];
for (i = 0; i<length; i++)//将每个数对应的最大子数组进行判断,最后得到整个整数组的最大子数组
{
for (j = 0; j<length; j++)
{
if (b[i][j]>temp)
{
temp = b[i][j];
p = i;
q = j;
}
}
}
cout << "最大子数组的值为:" << temp << endl;
cout << "最大子数组中元素的下标位子置:" << endl;
i = 0;
while (i <= q)
{
cout << p << " ";
p++;
if (p >= length)
{
p = 0;
}
i++;
}
cout << endl;
}
结果截图:
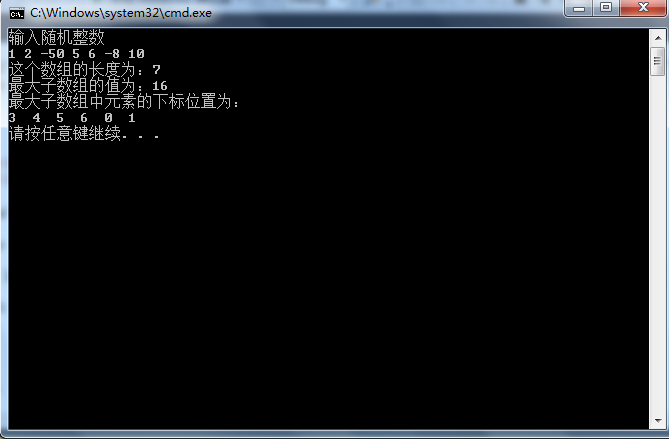
开发流程:
| 日期和任务 | 听课 | 看书 | 网上查资料 | 编程 | 日总计 |
| 周一 | 2 | 0 | 1 | 3 | |
| 周二 | 0 | ||||
| 周三 | 2 | 1 | 3 | ||
| 周四 | 2 | 2 | 4 | ||
| 周五 | 1 | 1 | 1 | 3 | |
| 周六 | 3 | 3 | 6 | ||
| 周日 | |||||
| 总计 | 4 | 3 | 6 | 6 | 19 |
总结:这次程序思想很重要,由环到线,由平常到特殊,要考虑的情况也要全面。
缺陷记录日志:未考虑数值超出范围是的情况




 本文介绍了一种解决环形数组中寻找最大子数组及其位置的方法,通过将环形数组转换为线性数组来简化问题,并给出了具体的实现代码。
本文介绍了一种解决环形数组中寻找最大子数组及其位置的方法,通过将环形数组转换为线性数组来简化问题,并给出了具体的实现代码。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








