对拉普拉斯平滑 的认识

拉普拉斯平滑是一个二阶微分的过程，简单地用图形解释为

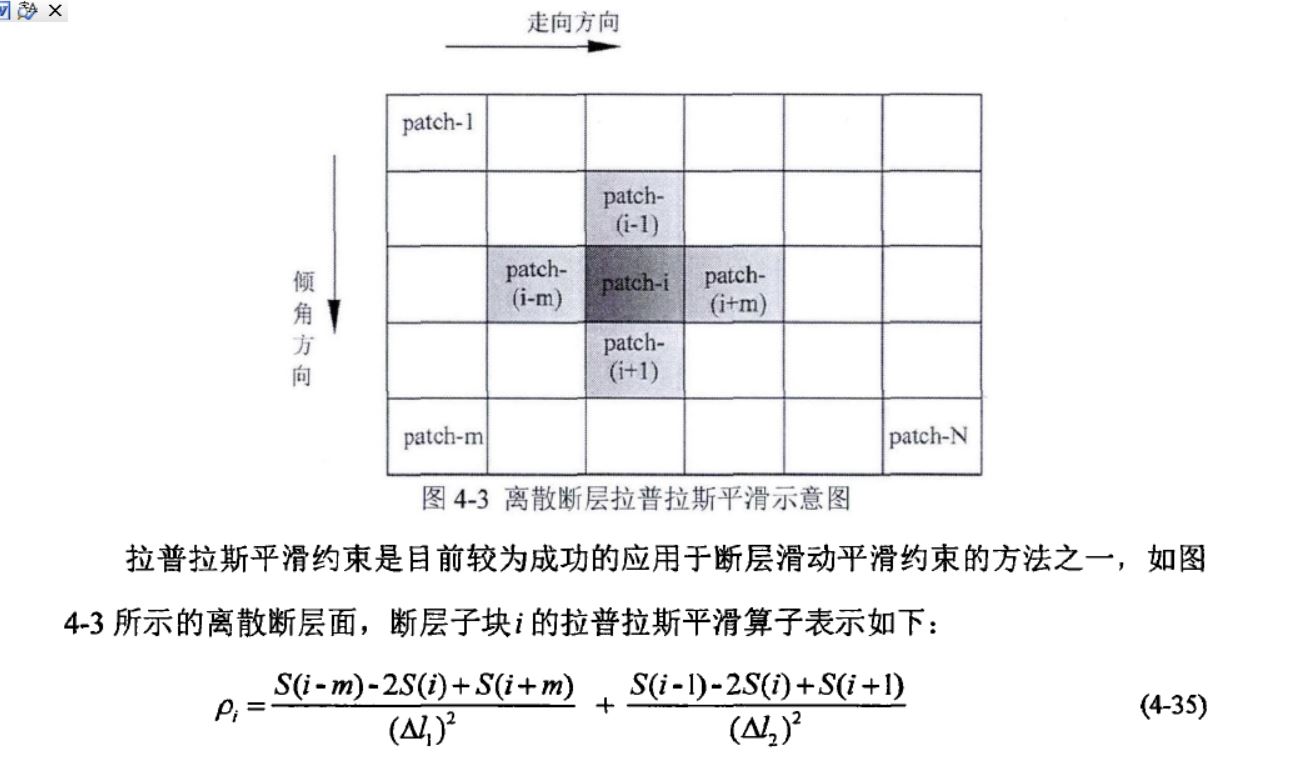
其实，要把其应用到实际中，其实就是求出的不同位置的S值的权重因子不同的问题；这样，我们来推：

(S(i,j)-S(i-1,j)-(S(i+1,j)-S(i,j)))/L是横着的二阶微分形式；

(S(i,j+1)-S(i,j)-(S(i,j+1)-S(i,j)))/w是竖着的二阶微分形式；

使S(i,j)=S0;S(i-1,j)=S1;S(i+1,j)=S3;S(i,j-1)=S2;S(i,j+1)=S4;

得到2*(L+W)/W*L*S0-1/W*S1-1/W*S4-1/L*S2-1/W*S3

因此就可以推导出它们之间的权重关系；

时间维度上：

S0为S1前一秒 ，S2为S1后一秒；

则S1-S0-(S2-S1)/(L/rupture_velcoity)和S1-S0-(S2-S1)/(W/rupture_velcoity)可以得到dip方向和strike方向。也可以得到S0与S1和S2之间的相对权重关系式。

当然，这是空间中心点旁边都有点，而时间维度也是三点连续的情况，二阶微分是可以满足的，但如果在边界呢，权重因子还不变吗？

转载于:https://www.cnblogs.com/seisjun/p/8108266.html