激活函数

1.Why

激活函数的作用: 用来加入非线性因素的，因为线性模型的表达能力不够。 如下一个单层感知机：

<img src="https://i-blog.csdnimg.cn/blog_migrate/e6a51b95e742bce55c64e6092bb60e95.png" data-rawwidth="884" data-rawheight="460" class="origin_image zh-lightbox-thumb" width="884" data-original="https://pic2.zhimg.com/2e83b4403f21654cd9147f13ecfaf799_r.png">

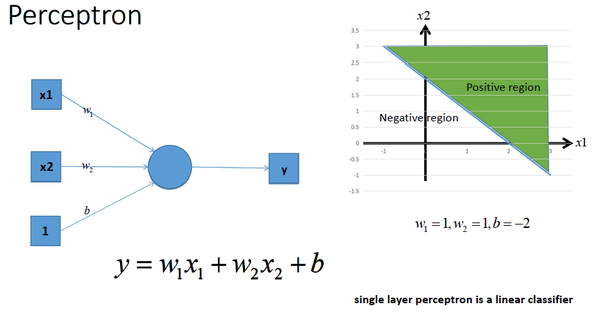
如果用多个感知机组合，能够获得更强的分类能力，：

<img src="https://i-blog.csdnimg.cn/blog_migrate/b29fa4771ee3ca2342ea9414d15b73d1.png" data-rawwidth="880" data-rawheight="459" class="origin_image zh-lightbox-thumb" width="880" data-original="https://pic2.zhimg.com/ef7eb0f56730058e1100dd6605eb2a25_r.png">那么我们动笔算一算, 就可以发现, 这样一个神经网络组合起来,输出的时候无论如何都还是一个线性方程哎~~~~纳尼, 说好的非线性分类呢~~~!!!!???

然而组合起来的形式还是一个线性方程：
　　

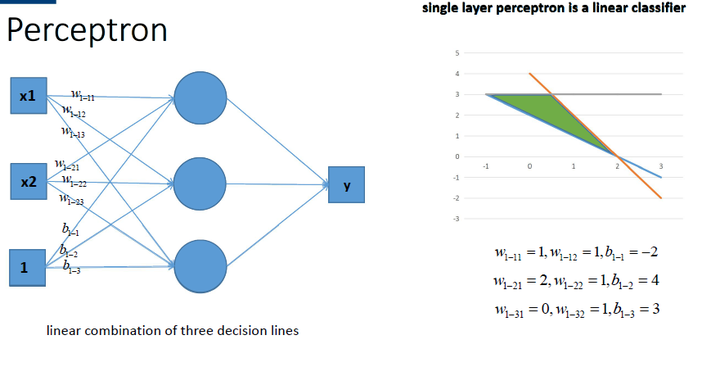
因此，提出了激活函数，在每层叠加完后，加一个激活函数，就变为非线性函数。。。

<img src="https://i-blog.csdnimg.cn/blog_migrate/c809f46f0a3e0506c9984b0ac7951b1f.png" data-rawwidth="923" data-rawheight="453" class="origin_image zh-lightbox-thumb" width="923" data-original="https://pic4.zhimg.com/3e4d3aabb90f51f467437a17861d3bf7_r.png">继续厚颜无耻地放一张跟之前那副图并列的图, 加上非线性激活函数之后, 我们就有可能学习到这样的平滑分类平面. 这个比刚刚那个看起来牛逼多了有木有!

2. what 

常用激活函数：（选取时保证可微）

1）tanh（双切正切函数）

• tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。
• 与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好。然而，tanh函数也存在梯度饱和问题，导致训练效率低下。

 

 

2）sigmoid（s型函数）

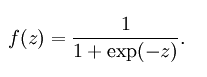
• 它可以将一个实数映射到(0,1)的区间，可以用来做二分类。

• 梯度饱和：当函数激活值接近于0或者1时，函数的梯度接近于0。当每层残差接近于0，计算出的梯度也不可避免地接近于0。这样在参数微调过程中，会引起参数弥散问题，传到前几层的梯度已经非常靠近0了

• 激活函数计算量大，反向传播求误差梯度时，求导涉及除法反向传播。

sigmoid 的导数表达式为：

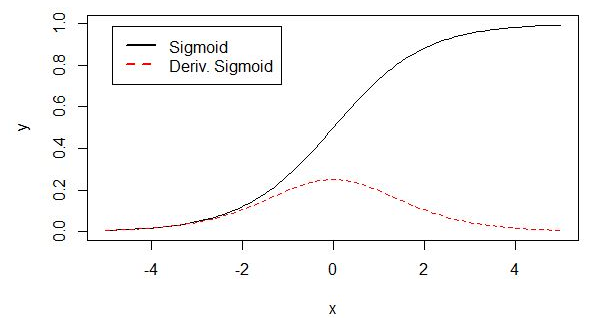
• 很容易就会出现梯度消失的情况，从而无法完成深层网络的训练

 

3）ReLU （简单，大于0的留下，否则为0） 用于隐层神经元输出

 

  ReLU 的导数：

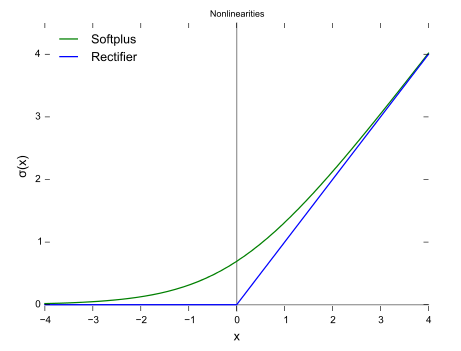
• 与sigmoid对比：

　　1）单侧抑制
　　2）相对宽阔的兴奋边界
　　3）稀疏激活性。

 

梯度不饱和：梯度计算公式为：1{x>0}，因此在反向传播过程中，减轻了梯度弥散的问题，神经网络前几层的参数也可以很快的更新。

计算速度快。正向传播过程中，sigmoid和tanh函数计算激活值时需要计算指数，而Relu函数仅需要设置阈值。如果x<0,f(x)=0，如果x>0,f(x)=x。加快了正向传播的计算速度。

• ReLU 的优点：

使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多

• 缺点：

训练的时候很”脆弱”，举个例子：由于ReLU在x<0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，也就是ReLU神经元坏死了，不再对任何数据有所响应。

 

4）Softmax - 用于多分类神经网络输出

为什么要取指数，第一个原因是要模拟 max 的行为，所以要让大的更大。
第二个原因是需要一个可导的函数。

 

转载于:https://www.cnblogs.com/fanhaha/p/7061318.html