实验六

最新推荐文章于 2024-05-25 21:43:14 发布

转载最新推荐文章于 2024-05-25 21:43:14 发布 · 76 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xinzhi999/p/10991397.html

本文深入探讨了C语言中的结构体与共同体概念，包括它们的定义、使用方法及区别。通过具体实例，展示了如何利用结构体进行学生信息管理和考试成绩处理，同时解释了共同体与结构体在内存分配上的不同之处。

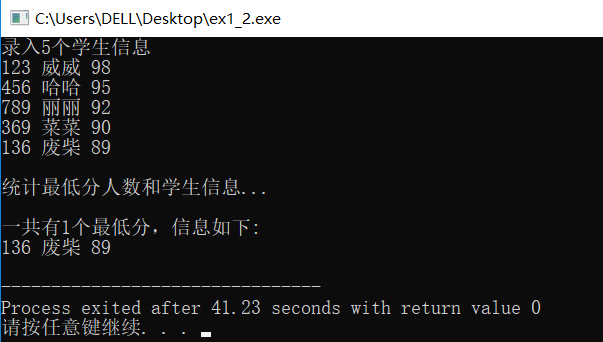
Part 1 统计最低分人数和信息

#include <stdio.h>

const int N=5;

// 定义结构体类型struct student,并定义STU为其别名 
typedef struct student {
    long no;
    char name[20];
    int score;     
}STU;

// 函数声明 
void input(STU s[], int n);
int findMinlist(STU s[], STU t[], int n);
void output(STU s[], int n);

int main() {
    STU stu[N], minlist[N];
    int count;
    
    printf("录入%d个学生信息\n", N);
    input(stu, N);
    
    printf("\n统计最低分人数和学生信息...\n");
    count = findMinlist(stu, minlist, N);
    
    printf("\n一共有%d个最低分，信息如下:\n", count);
    output(minlist, count);
     
    return 0;
} 

// 输入n个学生信息，存放在结构体数组s中 
void input(STU s[], int n) {
    int i;
    for(i=0; i<n; i++) 
        scanf("%ld %s %d", &s[i].no, s[i].name, &s[i].score);
} 

// 输出结构体s中n个元素信息
void output(STU s[], int n) {
    int i;
    for(i=0; i<n; i++)
        printf("%ld %s %d\n", s[i].no, s[i].name, s[i].score); 
} 

// 在结构体数组s中，查找最低分学生的记录，将其存入结构体数组s中
// 形参n是结构体数组s中元素个数
// 函数返回最低分的学生人数 
int findMinlist(STU s[], STU t[], int n) {
    int min,i,k=0;
    min=s[0].score;
    for(i=1;i<N;i++){
        if(s[i].score<min)
        min=s[i].score;}
    for(i=0;i<N;i++){
        if(min==s[i].score)
        t[k++]=s[i];}
        
        
     return k;    
    
}

运行结果：

Part 2 计算总分，确定等级：

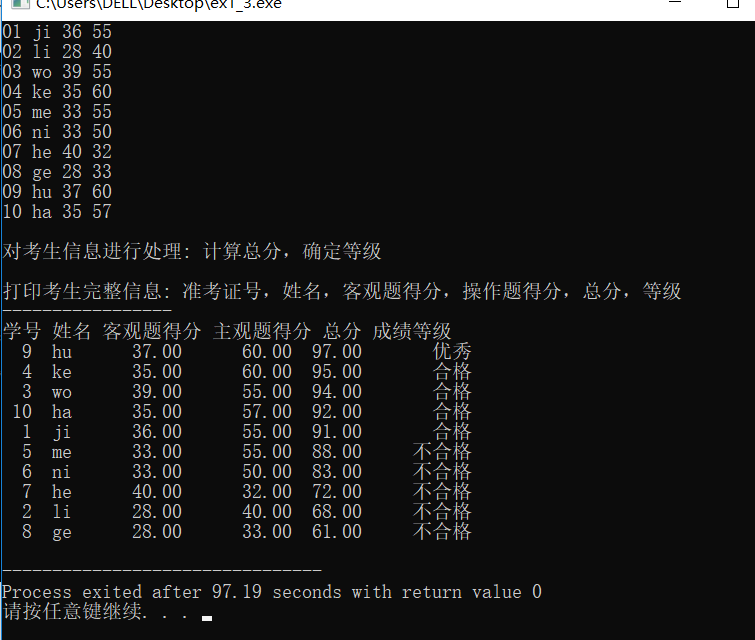
#include <stdio.h>
#include <string.h>
const int N = 10;

// 定义结构体类型struct student，并定义其别名为STU 
typedef struct student {
    long int id;
    char name[20];
    float objective;    /*客观题得分*/
    float subjective;    /*操作题得分*/
    float sum;
    char level[10];    
}STU; 

// 函数声明
void input(STU s[], int n);
void output(STU s[], int n);
void process(STU s[], int n);

int main() {
    STU stu[N];
    
    printf("录入%d个考生信息: 准考证号，姓名，客观题得分(<=40)，操作题得分(<=60)\n", N); 
    input(stu, N);
    
    printf("\n对考生信息进行处理: 计算总分，确定等级\n");
    process(stu, N);
    
    printf("\n打印考生完整信息: 准考证号，姓名，客观题得分，操作题得分，总分，等级\n");
    output(stu, N); 
    
    return 0;
} 

// 录入考生信息:准考证号，姓名，客观题得分，操作题得分
void input(STU s[], int n) {
    int i;
    for(i=0;i<n;i++){ 
    scanf("%d %s %f %f",&s[i].id,s[i].name,&s[i].objective,&s[i].subjective);
    }
}

//输出考生完整信息: 准考证号，姓名，客观题得分，操作题得分，总分，等级
void output(STU s[], int n) {
    int i;
    printf("-----------------\n");
   printf("学号 姓名 客观题得分 主观题得分 总分 成绩等级\n");
    for(i=0;i<n;i++)
    printf("%3d %3s %10.2f %10.2f %3.2f %10s\n",s[i].id,s[i].name,s[i].objective,s[i].subjective,s[i].sum,s[i].level); 
    
}

// 对考生信息进行处理：计算总分，排序，确定等级
void process(STU s[], int n) {
    int i,j,t=n*0.1,k=n*0.5;STU temp;
    for(i=0;i<n;i++){
    s[i].sum=s[i].objective+s[i].subjective;} 
    for(i=0;i<n-1;i++)
        for(j=0;j<n-1-i;j++)
        if(s[j].sum<s[j+1].sum){ 
        temp=s[j];
        s[j]=s[j+1];
        s[j+1]=temp;}    
            
    for(i=0;i<n;i++){
    if(s[i].sum>s[t].sum)
       strcpy(s[i].level,"优秀");
    else if(s[i].sum<=s[t].sum&&s[i].sum>s[k].sum)
        strcpy(s[i].level,"合格");
    else  if(s[i].sum<=s[k].sum)    
        strcpy(s[i].level,"不合格");}    
            
        
        
        
    }

运行结果：

Part 3 共同体与结构体的区别

共同体和结构体的表示方式不同：在一个结构体变量里，结构体各成员顺序排列存储，每个成员都有自己独立的存储位置；而一个共同体变量的所有成员共享同一片存储区域，一个共同体变量某一个时刻只能保存它的某一个成员的值。

Part 4 枚举变量使用过程中的注意事项能否直接输入输出？能否把一个int型数值赋值给一个枚举类型的变量？反过来呢？

1.枚举类型是一系列命名的整型常量，是一种基本的数据类型，并且用枚举类型描述的数据必须是有限个的。

2. 枚举变量不能直接的输入与输出。

3. 不能把一个int型数据直接赋值给枚举变量，若要赋值必须进行强制类型转换；反过来，一个枚举变量可以直接赋值给int型数据。

实验总结与体会

这一章是比较难的，学起来也比较费劲，许多看起来比较简单，但做起来还是比较难的，继续努力吧。

评论：1. https://www.cnblogs.com/a201883300049/p/11001185.html

2. https://www.cnblogs.com/74520qslm/p/11001090.html

3. https://www.cnblogs.com/yy-Siri/p/11000102.html

转载于:https://www.cnblogs.com/xinzhi999/p/10991397.html