课程作业02

一 . 使用计算机计算组合数：

1 . 使用组合数公式利用n!来计算

1 . 设计思想：

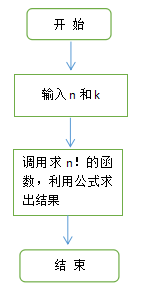
   首先解决求n！的函数，在主方法中调用，并利用公式进行输出

2 . 流程图：

3 . 源代码：

import java.util.Scanner;

public class Zuoye1

{

public static void main(String args[])

    {

       Scanner input=new Scanner(System.in);

       int n,k;//组合数公式中的n k

       System.out.println("请输入组合数公式的n和k：");

       n=input.nextInt();

       k=input.nextInt();

       long C=calculate(n)/(calculate(k)*calculate(n-k));

       System.out.println("结果为"+C);

    }

public static long calculate(int n)//计算n!的递归公式

    {

       if(n==1 || n==0)    return 1;

       return n*calculate(n-1);

    }

}

4 . 截图：

 

2 . 使用递推的方法用杨辉三角形计算

   1 . 设计思想：

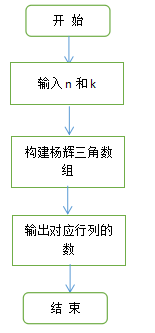
      输入n和k的值，创建一个二维数组，通过循环，在第一个循环里，定义i=1，在循环里嵌套循环，定义当j=0时，先判断j是否等于0或者i是否等于j，若成立则输出arr[i-1][j]=1,否则第i-1行j列的数等于第i-2行j列的数与第i-2行j-1列的数之和。最后输出结果。

   2 . 流程图：

3 . 源代码：

import java.util.Scanner;

public class Zuoye2

{

    public static void main(String args[])

    {

       Scanner input=new Scanner(System.in);

       int n,k;//组合数公式中的n k

       System.out.println("请输入组合数公式的n和k：");

       n=input.nextInt();

       k=input.nextInt();

       int [][]f=new int[27][27];//构建杨辉三角

        f[0][0] = 1;

        for(int i = 1;i <= 24;i++)

        {

            for(int j = 1;j <= i + 1;j++)

            {

                f[i][j] = f[i - 1][j - 1] + f[i - 1][j];

            }

        }

       System.out.println("结果为"+f[n+1][k+1]);//输出结果

    }

}.

4 . 截图：

3 . 使用递归的方法用组合数递推公式计算：

1 . 设计思想：

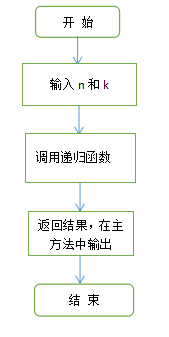
        类似于杨辉三角的思想，构造一个递归函数用来递归组合数，需要有两个参数。在主方法中写出输入n和k的语句，并在输出结果中调用递归函数，递归函数中，首先进行数字的判断，考虑特殊情况，当k=0或n=1或k=n时，输出都为1；当不是上述情况时，递归计算组合数。

 2 . 流程图：

3 . 源程序代码：

import java.util.Scanner;

public class Zuheshu

{

public static void main(String args[])

    {

       Scanner input=new Scanner(System.in);

       int n,k;

       System.out.println("请输入组合数公式的n和k：");

       n=input.nextInt();

       k=input.nextInt();

       System.out.println("结果为"+ZuHe(n,k));

    }

     static int ZuHe(int a,int b)

    {

       if(b==0)   return 1;

       else 

       {

           if(a==1)   return 1;

              else 

              {

                   if(a==b)      return 1;

                         else      return (ZuHe(a-1,b-1)+ZuHe(a-1,b));

              }

       }

    }

}

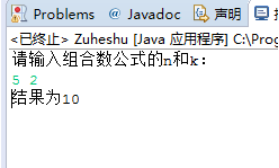
4 . 结果截图：

 

二 . 递归编程解决汉诺塔问题。用Java实现

1 . 设计思想：

        问题可以分为两个操作：一是将n-1个盘从一个座移到另一个座上，这是一个递归的过程，二是将一个盘子从一个座上移到另一个座上。用hanoi和move函数分别实现这两个操作，函数调用hanoi（n，one，two，three）表示将n个盘子从“one”座移到“three”座（借助two座），函数调用move（x，y）表示将一个盘子从x座移到y座的过程。x和y是代表A,B,C座之一，根据每次不同情况分别取A,B,C代入。

     2 . 流程图：

 

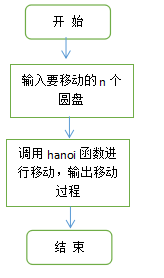
3 . 源代码：

import java.util.Scanner;

public class Hannuota

{

public static void main(String[] args)

{

int m;

System.out.println("请输入要移动的数量：");

Scanner input=new Scanner(System.in);

m=input.nextInt();

System.out.println("移动如下：");

hanoi(m,'A','B','C');

}

static void hanoi (int n,char one,char two,char three)

{

if(n==1)  move(one,three);

else

{

        hanoi(n-1,one,three,two);

        move(one,three);

        hanoi(n-1,two,one,three);

}

}

static void move(char x,char y)

{

System.out.println(x+"-->"+y);

}

}

4 . 截图：

 

三 . 使用递归方式判断某个字串是否是回文

1 . 设计思想：

输入一个字符串，首先定声明两个变量i和j，分别为字符串的第一个和最后一个字符，然后从头开始依次比较首尾字符，如果相同，再比较第二个和倒数第二个，依次比较直到最后完全相同，输出。

2 . 流程图：

 

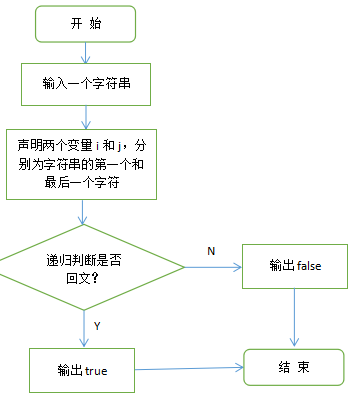
3 . 源代码：

import java.util.Scanner;

public class Huiwen

{

    public static void main(String args[])

    {

      Scanner input=new Scanner(System.in);

       String s=input.next();//输入字符串

       int i,j;

       i=0;//第一个字符

       j=s.length()-1;//最后一个字符

       System.out.println(HuiWen(s,i,j));

    }

    public static boolean HuiWen(String s,int i,int j)//判断字符串是否回文

    {

       if(i==j)

       {

           return true;

       }

       else if((i-1)==j)

       {

           return true;

       }

       return (s.charAt(i)==s.charAt(j))&&HuiWen(s,i+1,j-1);

    }

}

4 . 截图：

 

 

转载于:https://www.cnblogs.com/liboxun/p/7664306.html