拓扑排序

最新推荐文章于 2025-05-13 21:35:52 发布

转载最新推荐文章于 2025-05-13 21:35:52 发布 · 63 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/whileskies/p/6861853.html

本文详细介绍了拓扑排序的概念及其在有向无环图中的应用。文章通过定义拓扑序并提供了一个具体的算法实现来帮助读者理解如何进行拓扑排序。

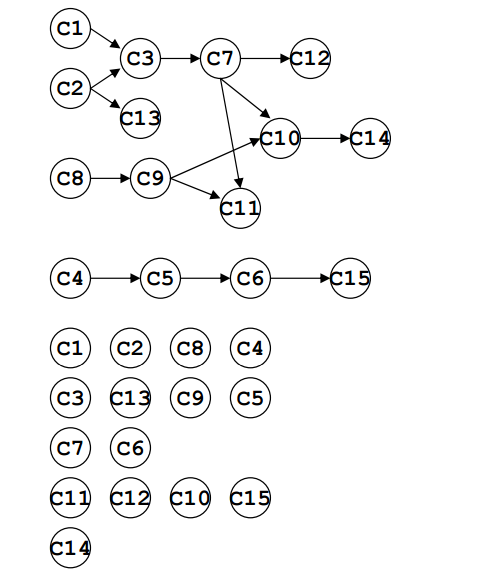
定义：

　　如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列成为一个拓扑序。

　　获得一个拓扑序的过程就是拓扑排序。

　　AOV(网络)如果有合理的拓扑序，则必定是有向无环图(Directed Acyclic Graph, DAG)

代码：

//邻接表存储
bool TopSort(LGraph Graph, Vertex TopOrder[])
{
    int InDegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
    Queue Q = CreatQueue(Graph->Nv);
    
    //初始化Indegree[]
    for (V = 0; V < Graph->Nv; V++)
        InDegree[V] = 0;
    //遍历图，得到Indegree[]
    for (V = 0; V < Graph->Nv; V++)
        for (W= Graph->G[V].FirstEdge; W; W=W->Next)
            InDegree[W->AdgV]++;
    //将所有入度为0的顶点入列
    for (V = 0; V < Graph->Nv; V++)
        if (InDegree[V] == 0)
            AddQ(Q, V);
    //拓扑排序
    cnt = 0;
    while (!IsEmpty(Q))
    {
        V = DeleteQ(Q);  //弹出一个度为0的元素
        TopOrder[cnt++] = V;
        //对V的每个邻接点W->AdjV
        for (W = Graph->G[V].FirstEdge; W; W=W->Next)
            if (--InDegree[W->AdjV] == 0)
                AddQ(Q, W->AdjV);
    }
    
    if (cnt != Graph->Nv)
        return false //图中有回路
    else
        return true;
}

转载于:https://www.cnblogs.com/whileskies/p/6861853.html