阶乘末尾连续零的个数

最新推荐文章于 2024-06-29 10:00:42 发布

转载最新推荐文章于 2024-06-29 10:00:42 发布 · 310 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/TianyuSu/p/9370237.html

本文介绍如何计算N!末尾连续零的个数，包括十进制和M进制的情况，并提供两种不同的计算方法及代码实现。

十进制中 N! 末尾连续零的个数

首先考虑 800 中有两个连续的零，800=$8*10^2$

首先考虑 50 中有一个连续的零，50= $5*10^1$

从上面可以看出，N! = $a*10^k$ , 那么 N! 末尾就有 $k$ 个连续的零
由质因数分解唯一定理，10 可以分解为小于10的质数乘积，即 10=2*5

所以我们只要统计出现 2，5的次数，取其中最小的即是末尾连续的零的个数

统计方法：

可以看出 2*5 产生一个0， 4*25产生两个零,8*125产生三个零，依次类推

例如：计算 2015! 中有多少连续的零
第一步，计算1到2015里多少个5,25,125,625
1、2015÷5=403 记作A1；
2、2015÷25=80.6取整得80 记作A2；
3、2015÷125=16.12取整得16 记作A3；
4、2015÷625=3.224取整得3 记作A4；
第二步，计算上述A1到A4中重复的部分
1、能被5整除的数里包含的能被25整除的数，记作B1
B1=A1-A2=403-80=323；
2、能被25整除的数里包含的能被125整除的数，记作B2
B2=A2-A3=80-16=64；
3、能被125整除的数里包含的能被625整除的数，记作B3
B3=A3-A4=16-3=13；
4、能被625整除的数里没有重复其它情况，直接计入结果，记作B4
B4=A4；
第三步，最终结果是
B11+B22+B33+B44=323+128+39+12=502.........(1)
另一种方法：
2015÷5+2015÷25+2015÷125+2015÷625=403+80+16+3=502。。。。。(2)

(1) (2)式子思路完全不同

(1)还需要使用容斥原理的知识去掉重复的部分

(2)式子为什么可以这么计算？

可以理解为，在计算 5 的个数时候，包含了 5 25， 125， 625

在计算25的个数时候，包含了 25 125 625

在计算125的个数时候，包含了125 625

在计算625的个数时候，包含了625

最终，5 计算一次，25计算2次，125计算3次，625计算4次

从上面可以看出来,计算零的个数时候, $51+252+1253+6254$ ，

正好和上面每次包含的数量是一致的，一次可以得到正确结果

对(2)的代码实现
```
//一种方法


int cnt_R_10_1(int n){
 int ans=0,mult=5;
 while(mult<=n){
     ans+=n/mult;
     mult*=5;
 }
 return ans;
}

//另一种方式，乘法的逆向思维
int cnt_R_10_2(int n){
 int ans=0;
 while(n){
     ans+=n/5;
     n/=5;
 }
 return ans;
}
```

M进制中 N! 末尾连续零的个数

有上面的例子我们可以推出

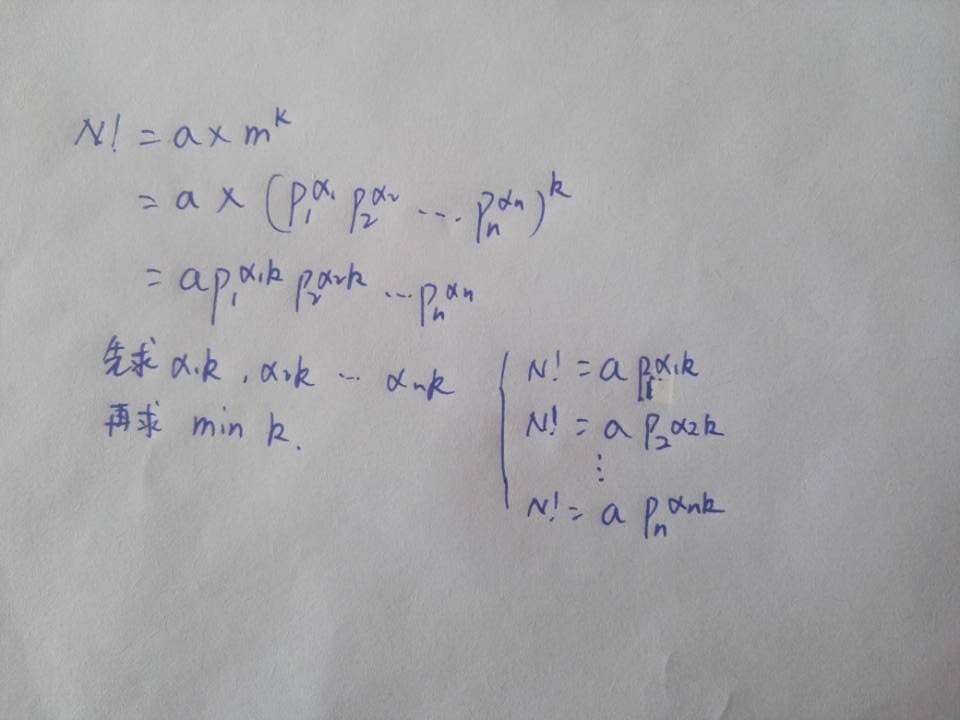
实现代码

#include "../common.h"
const int MAXN = 100;

//素数表
int prime[MAXN]={2};
//保存 alpha
int ind[MAXN]={0};
//保存 alpha·k 的乘积
int cnt[MAXN]={0};

//一种方式
int cnt_R_10_1(int n){
    int ans=0,mult=5;
    while(mult<=n){
        ans+=n/mult;
        mult*=5;
    }
    return ans;
}

//另一种方式，乘法的逆向思维
int cnt_R_10_2(int n){
    int ans=0;
    while(n){
        ans+=n/5;
        n/=5;
    }
    return ans;
}


void init(){
    int k=1;
    for(int i=3;i<=MAXN;i+=2){
        int flag=0;
        for(int j=2;j*j<=i;j++){
            if(i%j==0){
                flag=1; break;
            }
        }
        if(!flag)
            prime[k++]=i;
    }
}


//求 alpha·k 的乘积
int getcnt(int x, int p){
    int ans = 0;
    while(x){
        ans+=x/p;
        x/=p;
    }
    return ans;
}

int cnt_R_M(int n,int M){
    init();

    //看 M 可以被哪些质数分解
    for(int i=0;i<MAXN;i++){
        if(prime[i]){
            while(M % prime[i]==0){
            ind[prime[i]]++;
            M /= prime[i];
            }
        }       
    }


    for(int i=0;i<MAXN;i++){
        if(ind[i]) cnt[i]=getcnt(n,i);
    }

    int ans=1e8;
    for(int i=0;i<MAXN;i++){
        if(cnt[i]) ans=min(ans,cnt[i]/ind[i]);
    }

    return ans;

}


int main(int argc, char const *argv[])
{
    //求解十进制下 N! 中末尾连续零
    // cout<<"1: "<<cnt_R_10_1(2015)<<endl;
    // cout<<"2: "<<cnt_R_10_2(2015)<<endl;


    //2015! 在 M 进制下末尾连续零
    cout<<cnt_R_M(2015,10)<<endl;
    return 0;
}

转载于:https://www.cnblogs.com/TianyuSu/p/9370237.html