题目(1):最大连续子数组和(最大子段和)
背景
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
编写测试类
采用动态规划法,时间复杂度和空间复杂度都相对较少具体代码如下:
import java.util.*;
/**
*
* @author Bill
*
* 2018/03/29
*/
public class Maxsum {
public static int test(int[] array)
{
int [] maxsum=new int[1000];
int SUM=0;
int Count = array.length;
for(int i=1;i<Count;i++)
{
if(maxsum[i-1]>0)
maxsum[i]=maxsum[i-1]+array[i];
else
maxsum[i]=array[i];
if(maxsum[i]>SUM)
SUM=maxsum[i];
}
return SUM;
}
}
编写测试程序
测试程序主要运用条件组合覆盖来对测试类测试,具体代码如下:
import static org.junit.Assert.*;
import org.junit.Test;
public class MaxsumTest {
@Test
public void test() {
int[] sum=new int[]{-4,-1,-4,-10,-5,-1};//均为负数时
int s=new Maxsum().test(sum);
assertEquals(0,s);
}
@Test
public void test1() {
int[] sum=new int[]{1,2,-3,4,5,6,-7};
int s1=new Maxsum().test(sum);
assertEquals(15,s1);
}
@Test
public void test2() {
int[] sum=new int[]{-1,-2,-23,-14,-5,67,-7};
int s2=new Maxsum().test(sum);
assertEquals(67,s2);
}
@Test
public void test3() {
int[] sum=new int[]{-1,-14,5,-67};
int s3=new Maxsum().test(sum);
assertEquals(23,s3);
}
}
测试结果
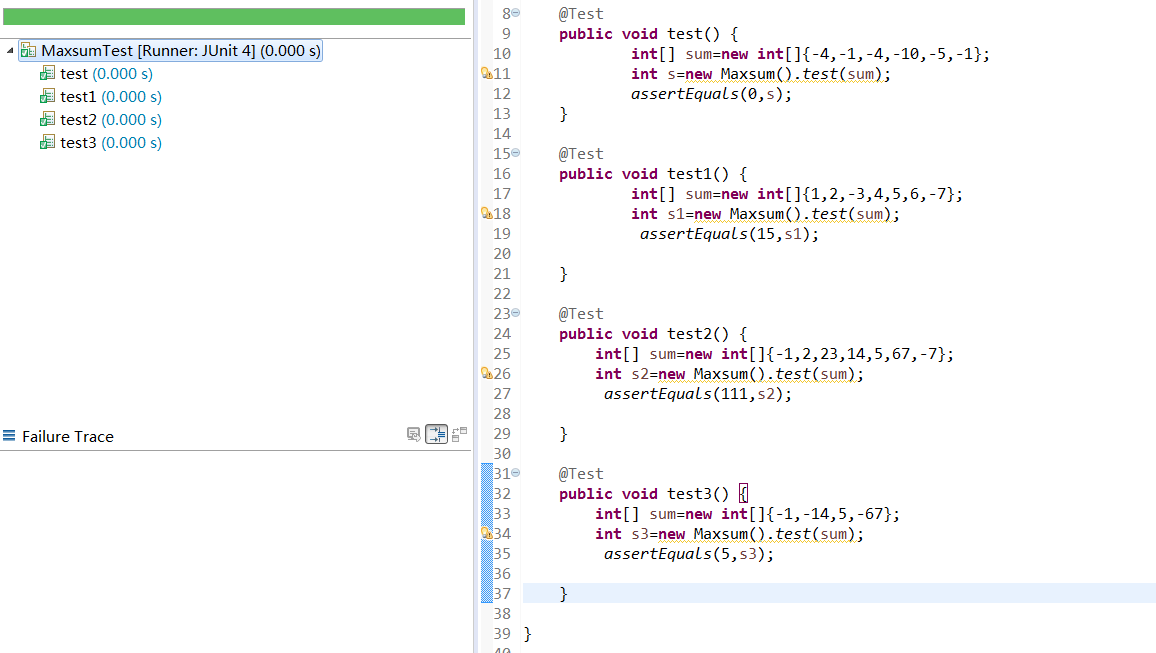







 本文介绍了最大子段和问题的解决方法,并通过动态规划法实现了最大连续子数组和的计算。提供了具体的Java实现代码及测试用例,帮助读者理解和验证算法的有效性。
本文介绍了最大子段和问题的解决方法,并通过动态规划法实现了最大连续子数组和的计算。提供了具体的Java实现代码及测试用例,帮助读者理解和验证算法的有效性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








