Hausdorff Distance(豪斯多夫距离)

 

　　Hausdorff Distance(豪斯多夫距离)

参考博客：
http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html

理解：

　　Hausdorff距离是描述两组点集之间相似程度的一种量度，它是两个点集之间距离的一种定义形式。

　　假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为

　　H(A,B)=max(h(A,B),h(B,A))                    (1)

　　其中,

　　h(A,B)=max（a∈A）min（b∈B）‖a-b‖     (2)

　　h(B,A)=max（b∈B）min（a∈A）‖b-a‖     (3)

　　‖·‖是点集A和B点集间的距离范式(如:L2或Euclidean距离).

　　这里,式(1)称为双向Hausdorff距离,是Hausdorff距离的最基本形式;式(2)中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离.即h(A,B)实际上首先对点集A中的每个点ai到距离此点ai最近的B集合中点bj之间的距离‖ai-bj‖进行排序,然后取该距离中的最大值作为h(A,B)的值.h(B,A)同理可得.

　　由式(1)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了两个点集间的最大不匹配程度.

 

以下是参考文献的摘录：

1.Introduction
　　When talking about distances, we usually mean the shortest : for instance, if a point X is said to be at distance D of a polygon P, we generally assume that D is the distance from X to the nearest point of P..

　　The same logic applies for polygons : if two polygons A and B are at some distance from each other, we commonly understand that distance as the shortest one between any point of A and any point of B.

　　Formally, this is called a minimin function, because the distance D between A and B is given by :

　　 

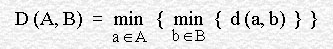
　　即 A集合中的任一点ai 到集合B中的任意点的最短的距离di，然后在这些距离di中选择距离最短的，即作为两个集合A与B的距离。

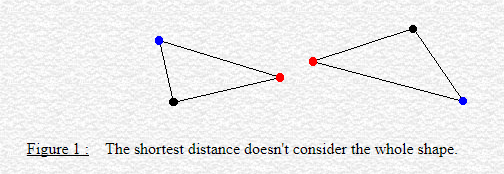
　　That definition of distance between polygons can become quite unsatisfactory for some applications （并不适用于描述两个多边形的位置关系）;  let's see for example fig. 1.  We could say the triangles are close to each other considering their shortest distance, shown by their red vertices. However, we would naturally expect that a small distance between these polygons means that no point of one polygon is far from the other polygon.   In this sense, the two polygons shown in fig. 1 are not so close, as their furthest points, shown in blue, could actually be very far away from the other polygon. Clearly, the shortest distance is totally independent of each polygonal shape.

　　

　　另一个例子：

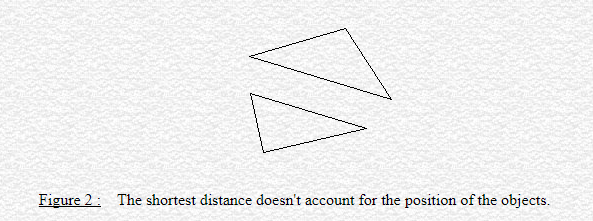
　　Another example is given by fig. 2, where we have the same two triangles at the same shortest distance than in fig. 1, but in different position.  It's quite obvious that the shortest distance concept carries very low informative content, as the distance value did not change from the previous case, while something did change with the objects.

　　两个多边形的最短距离提供的信息很少。 如下图，与图1同样最短距离的两个多边形的位置却不同。

　　

　　因此：

　　 定义Hausdoff Distance 距离可以捕捉两个多边形的细微之处， 因此要忽略其最短距离。

2.  Hausdoff Distance 定义

　　More formally, Hausdorff distance from set A to set B is a maximin function, defined as

　　

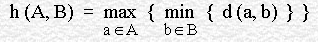
　　where a and b are points of sets A and B respectively, and d(a, b) is any metric between these points ; for simplicity, we'll take d(a, b) as the Euclidian distance between a and b. If for instance A and B are two sets of points, a brute force algorithm would be :

　　即： 即 A集合中的任一点ai 到集合B中的任意点的最短的距离di，然后在这些距离di中选择距离