0x03 递归

最新推荐文章于 2024-11-10 23:46:02 发布

转载最新推荐文章于 2024-11-10 23:46:02 发布 · 54 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/AKCqhzdy/p/9063644.html

本文介绍了一种使用矩阵快速幂求解特定数学问题的方法，并实现了一个分形搜索算法来解决复杂的数据结构问题。文章提供了详细的代码示例，包括矩阵操作、快速幂运算以及分形结构的递归搜索。

这个东西好像在搞矩乘的时候用过？忘了

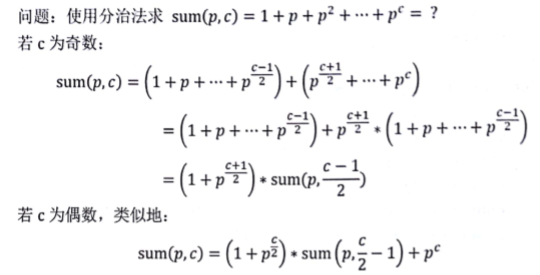
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const int mod=9901;

int len;LL zy[110],cs[110];
void get_zy(LL n)
{
    len=0;
    for(LL i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            len++;
            zy[len]=i;cs[len]=0;
            while(n%i==0)n/=i,cs[len]++;
        }
    }
    if(n>1) len++, zy[len]=n, cs[len]=1;
}

//---------------------------------

LL quick_power(LL n,int p)
{
    LL A=n%mod,ret=1;
    while(p>0)
    {
        if(p%2==1)ret=(ret*A)%mod;
        A=(A*A)%mod;p/=2;
    }
    return ret;
}
LL fenzi(LL n,int p)
{
    if(p==0)return 1;
    if(p%2==0)
    {
        return (( fenzi(n,p/2-1)*(1+quick_power(n,p/2)) )%mod+quick_power(n,p))%mod;
    }
    else
    {
        return ( fenzi(n,p/2)*(1+quick_power(n,p/2+1)) )%mod;
    }
}
int main()
{
    LL n;int p;
    while(scanf("%lld%d",&n,&p)!=EOF)
    {
        get_zy(n);
    
        LL ans=1;
        for(int i=1;i<=len;i++)
        {
            ans=(ans*fenzi(zy[i],cs[i]*p))%mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

poj1845

3889那题太无聊了，题意还贼难理解，YY了下做法，就是很裸分治找在那个位置，维护横纵区间

手工栈太麻烦了，看这题吧bzoj2819Nim 但是好像机友们只传1个参数的搜索也可以

总的来讲没什么意思。

upd：

填坑：poj3889一道分形题，这种通过搜索变量交换进行翻转的题挺好的。反正自己肯定看得懂就不详写了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL; 

LL Bin[40];
void dfs(LL n,LL k,LL &x,LL &y)
{
    if(n==1)
    {
        if(k==1)x=1,y=1;
        else if(k==2)x=1,y=2;
        else if(k==3)x=2,y=2;
        else x=2,y=1;
        return ;
    }
    
    LL d=Bin[n-1]*Bin[n-1];
    if(k<=d)//左上 
    {
        dfs(n-1,k,y,x);
    }
    else if(k<=2*d)//右上 
    {
        dfs(n-1,k-d,x,y);
        y+=Bin[n-1];
    }
    else if(k<=3*d)//右下 
    {
        dfs(n-1,k-2*d,x,y);
        x+=Bin[n-1];y+=Bin[n-1];
    }
    else//左下 
    {
        dfs(n-1,k-3*d,y,x);
        x=Bin[n]+1-x;y=Bin[n-1]+1-y;
    }
}

int main()
{
    Bin[0]=1;for(int i=1;i<=31;i++)Bin[i]=Bin[i-1]*2LL;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n,st,ed;
        scanf("%lld%lld%lld",&n,&st,&ed);
        LL stx,sty,edx,edy;
        dfs(n,st,stx,sty),dfs(n,ed,edx,edy);
        printf("%.0lf\n",sqrt(double((stx-edx)*(stx-edx)+(sty-edy)*(sty-edy)))*10);
    }
    return 0;
}