POJ_1227 Jack Straws 【二维平面判两线段相交】

最新推荐文章于 2022-01-14 19:42:18 发布

weixin_30338743

最新推荐文章于 2022-01-14 19:42:18 发布

阅读量139

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/dybala21/p/10856934.html

一　题面

　　POJ1127

二　分析

　　在平面几何中，判断两线段相交的方法一般是使用跨立实验。但是这题考虑了非严格相交，即如何两个线段刚好端点相交则也是相交的，所以还需要使用快速排斥实验。

　　这里参考并引用了 TangMoon 博客。

　　1.快速排斥实验

　　由于两个点作为矩形的两个斜对角线端点可以确定一个矩形，则根据两个点确定一个向量，两个向量显然可以确定两个矩形。

　　对于快速排斥实验，也可尝试逆向思维，如果判断让两个向量确定的两个矩形是否相交部分，相当于判断两个矩形没有相交部分的反。

　　具体条件就是a.其中一个矩形的最小横坐标大于另一个矩形的最大横坐标；b.其中一个矩形的最小纵坐标大于另一个矩形的最大纵坐标。

　　2.跨立实验

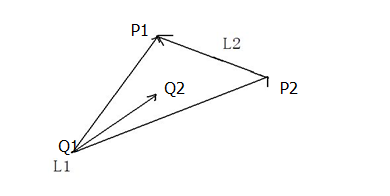
　　如图，根据以$Q1$为起点

${\overrightarrow{Q_{1}P_{2}} }\times {\overrightarrow{Q_{1}Q_{2}}}$

${\overrightarrow{Q_{1}Q_{2}} }\times {\overrightarrow{Q_{1}P_{1}}}$

　　判断这两个向量的正负，如果两个值正负相同，表示$\overrightarrow{Q_{1}Q_{2}}$在两向量中间，但这显然还不够，因为可能$Q2$没跨过去，所以还需要在$P1$判断一次。

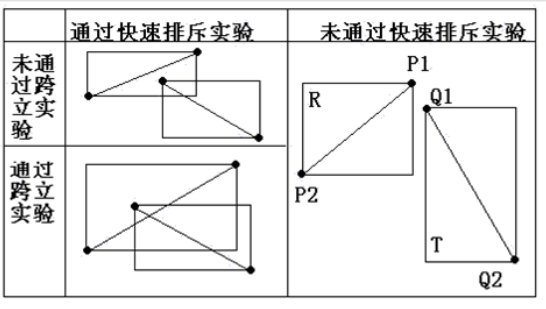
　　那么这样把上述两条件都判断后，就能保证两线段非严格相交了。

三　AC代码

  1 #include <iostream>
  2 #include <cstring>
  3 #include <cstdio>
  4 
  5 using namespace std;
  6 const int MAXN = 200;
  7 struct P
  8 {
  9     int a, b;
 10     P(){}
 11     P(int x, int y): a(x),b(y){}
 12     P operator + (P t)
 13     {
 14         return P(a + t.a, b + t.b);
 15     }
 16     P operator - (P t)
 17     {
 18         return P(a - t.a, b - t.b);
 19     }
 20     P operator * (P t)
 21     {
 22         return P(a*t.a, b*t.b);
 23     }
 24     int dot(P t)
 25     {
 26         return a*t.a + b*t.b;
 27     }
 28     int det(P t)
 29     {
 30         return a*t.b - b*t.a;
 31     }
 32 };
 33 int px[MAXN], py[MAXN];
 34 int qx[MAXN], qy[MAXN];
 35 
 36 bool solve(int t1, int t2)
 37 {
 38     if(min(px[t1], qx[t1]) > max(px[t2], qx[t2]) || min(px[t2], qx[t2]) > max(px[t1], qx[t1]) 
 39         || min(py[t1], qy[t2]) > max(py[t2], qy[t2]) || min(py[t2], qy[t2]) > max(py[t1], qy[t1]))
 40         return false;
 41     P p1, p2, p3;
 42     p1 = P(qx[t1]-px[t2], qy[t1]-py[t2]);
 43     p2 = P(qx[t2]-px[t2], qy[t2]-py[t2]);
 44     p3 = P(px[t1]-px[t2], py[t1]-py[t2]);
 45     if(p1.det(p2) * p2.det(p3) < 0)
 46         return false;
 47     p1 = P(px[t2]-px[t1], py[t2]-py[t1]);
 48     p2 = P(qx[t1]-px[t1], qy[t1]-py[t1]);
 49     p3 = P(qx[t2]-px[t1], qy[t2]-py[t1]);
 50     if(p1.det(p2) * p2.det(p3) < 0)
 51         return false;
 52     return true;
 53 }
 54 
 55 int par[MAXN];
 56 
 57 int find(int x)
 58 {
 59     return par[x] == x ? x : par[x] = find(par[x]);
 60 }
 61 void unite(int x, int y)
 62 {
 63     int f1 = find(x), f2 = find(y);
 64     if(f1 == f2)
 65         return;
 66     else
 67         par[f1] = f2;
 68 }
 69 
 70 
 71 int main()
 72 {
 73     //freopen("input.txt", "r", stdin);
 74     int n;
 75     while(scanf("%d", &n) == 1)
 76     {
 77         
 78         if(n == 0)  break;
 79         for(int i = 1; i <= n; i++)
 80         {
 81             par[i] = i;
 82             scanf("%d%d%d%d", &px[i], &py[i], &qx[i], &qy[i]);
 83         }
 84         for(int i = 1; i <= n; i++)
 85             for(int j = i + 1; j <= n; j++)
 86             {
 87                 if(solve(i, j))
 88                     unite(i, j);
 89             }
 90         int x, y;
 91         while(scanf("%d%d", &x, &y) != EOF)
 92         {
 93             if(x == 0)  break;
 94             if(find(x) == find(y))
 95                 printf("CONNECTED\n");
 96             else
 97                 printf("NOT CONNECTED\n");
 98         }
 99     }
100     return 0;
101 }