KMP注记

最新推荐文章于 2024-10-20 09:00:00 发布

转载最新推荐文章于 2024-10-20 09:00:00 发布 · 53 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/chenyliang/p/8658637.html

相关介绍在下面:

https://blog.youkuaiyun.com/yutianzuijin/article/details/11954939
http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html
实际上，最先看的是2，但并描述没那么清晰，1上的图描述易于理解。这里保存一下。注释见图注。

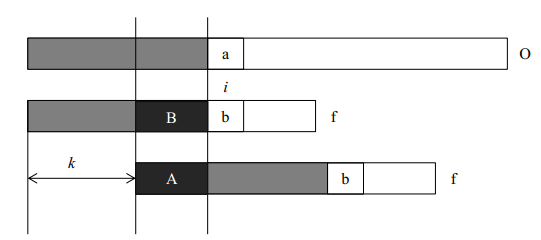
Fig 1. O是待搜索串， f是模式串。如果在 i处没有匹配上，可以已知在该处之前有一定长度的后缀与O对应上（就是B段），所以如果有 next表的协助，可以知道将f后移多少（就是 k），能够匹配上这段后缀对应上O的字段。

要求next保存最长后缀，是避免回溯的关键环节（比如，考虑一下next中元素始终为0(除首个)，那么每次j重置后依然不能匹配到i上，算法直接失败）。
关于对f进行移动这点，是1中没有表达的，但这一点更易于理解（好吧大佬们，对我而言(⊙﹏⊙)b）。

def genNext(s, nextTab=None, idx=0):
    assert idx>=0, idx
    if nextTab is None:
        nextTab = [0 for i in s]
    if idx==len(nextTab):
        return nextTab
    if idx ==0:
        nextTab[idx] = -1
    # fill the idx-th element...
    else:
        if s[nextTab[idx-1]+1] == s[idx]:
            nextTab[idx] = nextTab[idx-1] +1
        else:
            nextTab[idx] = 0
    return genNext(s,nextTab, idx+1)

s='ababcababa'
p='ababa'

print s
print p
print genNext(p)



def searchPat(s,p):
    nextTab = genNext(p)
    j=0
    i=0
    while True:
        if s[i]==p[j]:
            j+=1
            i+=1
        elif nextTab[j] >=0:
            j=nextTab[j]
        elif nextTab[j]==-1:
            i += 1
            j = 0
#        print i,j
        if j==len(p):
            return i-j
    return -1
print searchPat(s,p)

转载于:https://www.cnblogs.com/chenyliang/p/8658637.html