Machine Learning - Coursera week5 cost function and backpropagation 2-优快云博客

本文介绍了神经网络的成本函数及其简化形式，并详细解释了反向传播算法的工作原理，包括如何通过计算δ值来衡量预测结果与实际结果之间的误差。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 回顾cost function

cost function for a neural network is:
J(Θ)=−1m∑t=1m∑k=1K[y(t)k log(hΘ(x(t)))k+(1−y(t)k) log(1−hΘ(x(t))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2

simple non-multiclass classification (k = 1) and disregard regularization, the cost is computed with:

cost(t)=y(t)log(hΘ(x(t))+(1−y(t))log(1−hΘ(x(t))

Theδ(l)j is the error for a(l)j ,

δ j (l) = \partial c o s t ( t ) \partial z ( l ) j

2. 计算δ(l)j

回顾一下前向传播，某一个节点的值是如何计算的。我们将把(xi，yi )输入到这个网络当中, x1i和x2i将是我们对输入层的设置. 当我们进入第一个隐层，我们会计算z(2)1和z(2)2.然后我们来用冲击函数计算他们的激励值有a(2)1和a(2)2。之后我们把这些值乘以相应的权重如θ(2)10,θ(2)11,θ(2)12并赋予给z(3)1，再使用sigmoid函数激活得到a(3)1。类似的，我们一直得到z(4)1和最后的结果a(4)1.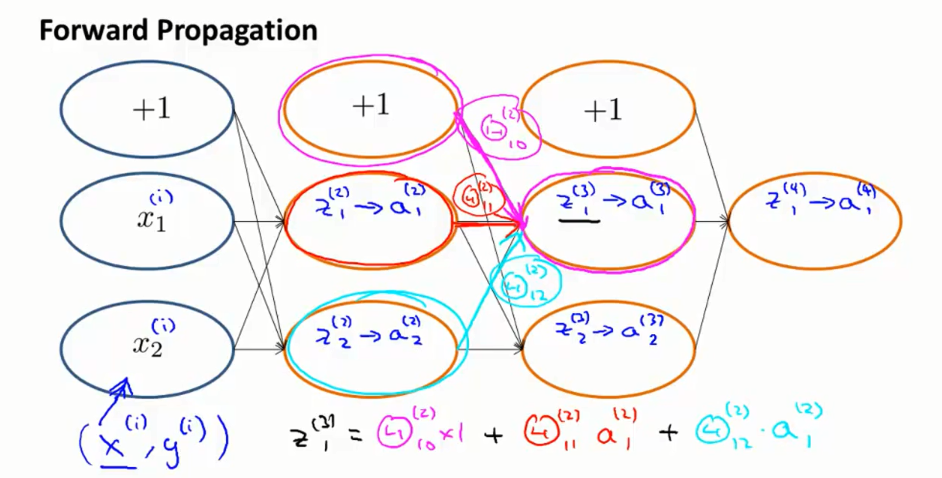

误差反向传播与正向传播很像，我们先看他的代价函数。考虑最简单的一个输出（K=1）的情况：
J(Θ)=−1m∑t=1m[y(t) log(hΘ(x(t)))+(1−y(t)) log(1−hΘ(x(t)))]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2
不考虑正则化:

J (Θ) = - 1 m \sum t = 1 m [y (t) log (h Θ (x (t))) + (1 - y (t)) log (1 - h Θ (x (t)))]

上面简化的代价函数所做的事情就和下面的函数是一样的：

c o s t (t) = y (t) l o g (h Θ (x (t)) + (1 - y (t)) l o g (1 - h Θ (x (t))

这个函数的作用等价于逻辑回归时使用的均方误差，描述模型的输出和真实值的接近程度。

反向传播在做什么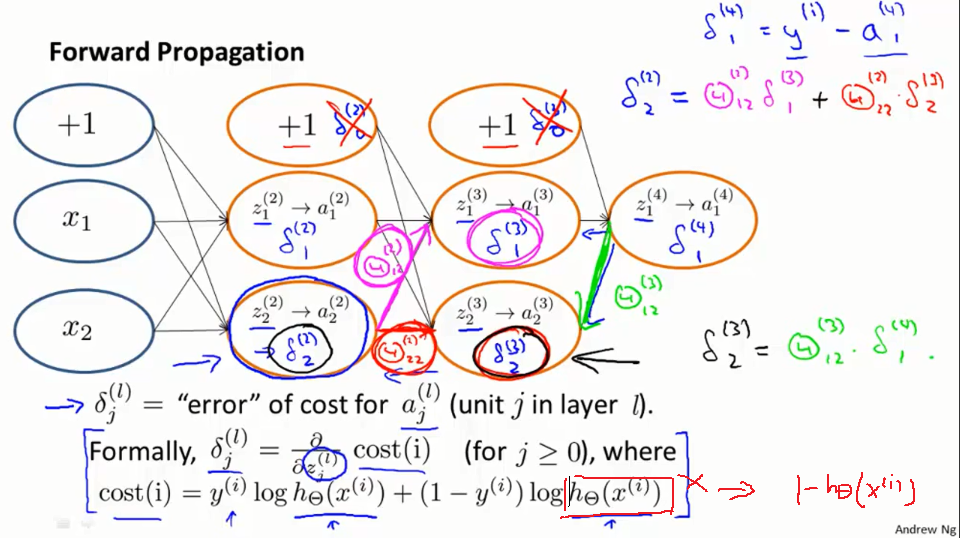

首先，设置delta项 δ(4)1,正如我们对前向传播算法对训练数据i的做法一样。 δ(4)1=a(4)1−yi就是我们预测结果和真实结果的误差。我们 δ(4)1反向传播回去，得到 δ(3)1, δ(3)2. 进一步往前，得到 δ(21和 δ(2)2. 看起来就像是前向传播,只不过我们现在反过来做了. 看看最后我们如何得到δ(2)2. 所以我们得到δ(2)2 和前向传播类似，它与权重Θ(211和 Θ(2)22，以及下一层的误差结果δ(3)1, δ(3)2相关，把这个值乘以它权值，最后做加权求和就得到了δ(2)2。同理这里还要知道δ(3)2，这就等于δ(4)1乘以它的权重。我们一般不考虑偏置单元。