homework3:课本习题练习

首先，本次要求是找出质数，书上给的代码如下：

    private static void printPrimes (int n) 
    { 
        int curPrime; // Value currently considered for primeness 
        int numPrimes; // Number of primes found so far. 
        boolean isPrime; // Is curPrime prime? 
        int [] primes = new int [MAXPRIMES]; // The list of prime numbers. 
        
        // Initialize 2 into the list of primes. 
        primes [0] = 2; 
        numPrimes = 1; 
        curPrime = 2; 
        while (numPrimes < n) 
        { 
            curPrime++; // next number to consider ... 
            isPrime = true; 
            for (int i = 0; i <= numPrimes-1; i++) 
            { // for each previous prime. 
                if (isDivisable(primes[i],curPrime)) 
                { // Found a divisor, curPrime is not prime. 
                    isPrime = false; 
                    break; // out of loop through primes. 
                } 
            } 
            if (isPrime) 
            { // save it! 
                primes[numPrimes] = curPrime; 
                numPrimes++; 
            } 
        } // End while 
        
        // Print all the primes out. 
        for (int i = 0; i <= numPrimes-1; i++) 
        { 
            System.out.println ("Prime: " + primes[i]); 
        } 
    } // end printPrimes

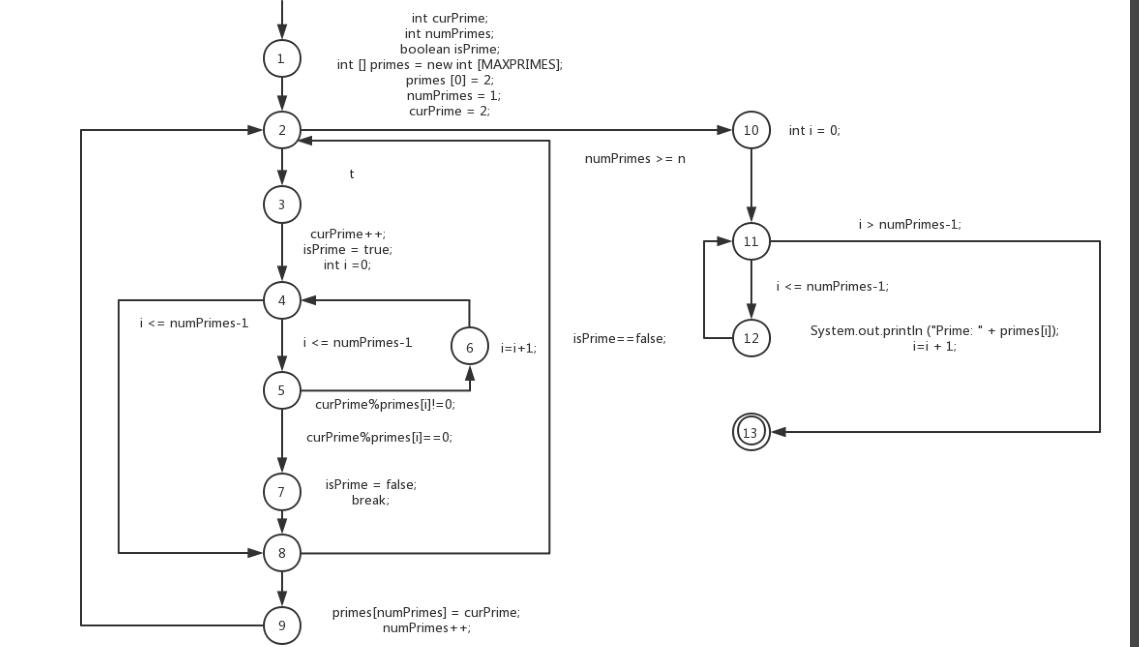
问题1：画出该方法的控制流图

答：如下。

 

 

问题2:考虑测试用例t1=(n=3)和t2=(n=5)。即使这些测试用例经过printfPrimes()方法中相同的主路径，他们不一定找出相同的错误。设计一个简单的错误，使得t2比t1

更容易发现。

答：数组越界时可能会发生错误，如令MAXPRIMES=4。

 

问题3：找到一个测试用例，使得测试路径不用通过while循环体。

答：令初始条件n=1。

 

问题4：列举每个节点覆盖，边覆盖和主路径覆盖的测试需求。

      点覆盖: {1,2,3,4,5,6,7,8,9,10,11,12}

　　边覆盖:{(1,2),(2,3),(2,10),(3,4),(4,5),(4,8),(5,6),(5,7),(6,4),(7,8),(8,2),(8,9),(9,2),(10,11),(10,12),(11,10)}

　　主路径覆盖: {(1,2,3,4,5,6),

　　　　　　　　 (1,2,3,4,5,7,8,9),

　　　　　　　　 (1,2,10,11),

　　　　　　　　 (1,2,10,12),

　　　　　　　　 (2,3,4,5,7,8,9,2),

　　　　　　　　 (2,3,4,5,7,8,2)

　　　　　　　　 (2,3,4,8,9,2),

　　　　　　　　 (2,3,4,8,2)

　　　　　　　　 (3,4,5,7,8,9,2,10,11,12),

　　　　　　　　 (3,4,5,7,8,9,2,10,11,13),

　　　　　　　　 (3,4,5,7,8,2,10,11,12),

　　　　　　　　 (3,4,5,7,8,2,10,11,13),

　　　　　　　　 (4,5,6,4),

　　　　　　　　 (4,5,7,8,9,2,3,4),

　　　　　　　　 (4,5,7,8,2,3,4),

　　　　　　　　 (4,8,2,3,4),

　　　　　　　　 (4,8,9,2,3,4),

　　　　　　　　 (5,6,4,5),

　　　　　　　　 (5,6,4,8,9,2,10,11,12),

　　　　　　　　 (5,6,4,8,9,2,10,11,13),

　　　　　　 　　(5,6,4,8,2,10,11,12),

　　　　　　　　 (5,6,4,8,2,10,11,13),

　　　　　　　　 (6,4,5,6),

　　　　　　　　 (6,4,5,7,8,9,2,10,11,12),

　　　　　　　　 (6,4,5,7,8,9,2,10,11,13),

　　　　　　　　 (6,4,5,7,8,2,10,11,12),

　　　　　　　　 (6,4,5,7,8,2,10,11,13),

　　　　　　　　 (6,4,5,7,8,9,2,3),

　　　　　　　　 (6,4,8,9,2,3),

　　　　　　　　 (7,8,9,2,3,4,5,7),

　　　　　　　　 (7,8,2,3,4,5,7),

　　　　　　　　 (8,9,2,3,4,5,7,8),

　　　　　　　　 (8,2,3,4,5,7,8),

　　　　　　　　 (8,9,2,3,4,8),

　　　　　　　　 (8,2,3,4,8),

　　　　　　　　 (9,2,3,4,5,7,8,9),

　　　　　　　　 (9,2,3,4,8,9),

　　　　　　　　 (11,12,11),

　　　　　　　　 (12,11,12),

　　　　　　　　 (12,11,13)

}

 

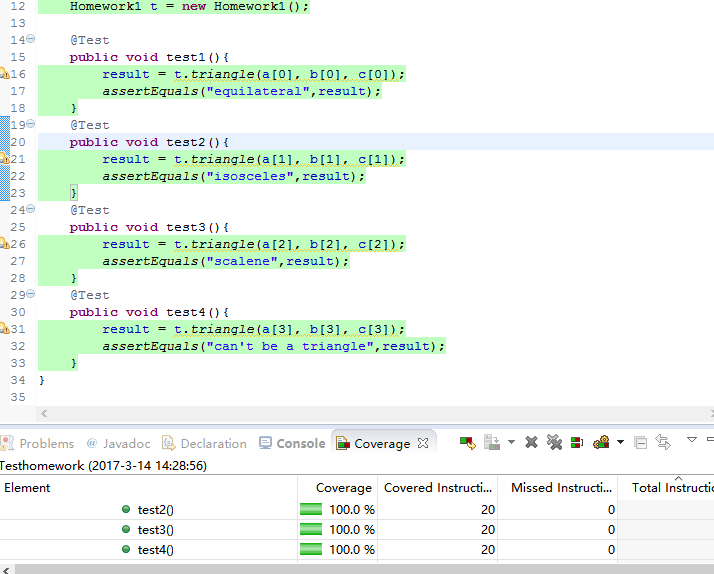
问题5：基于Junit及Eclemma（ jacoco）实现一个主路径覆盖的测试。

可以用上次实验一的三角形程序进行主路径覆盖测试。

考虑等边三角形，等腰三角形，不等边三角形和不能组成三角形这四种情况，覆盖率达到了100%。

 

转载于:https://www.cnblogs.com/cricketvaxes/p/6545256.html