CSAPP笔记(第二章 信息的表示和处理)-02

第二章内容为p58~p124

概要

本章的后半部分讲了整数的二进制(原码和补码)的四则运算, 以及浮点数的四则运算.

整数的二进制四则运算

w位的2个二进制数相加减, 结果的范围需要w+1位来存储, 而实际中位数是固定的, 结果超出w位表达的范围产生"溢出", 计算机需要处理这种"溢出", 就称为本部分的主要内容.

加减法

• w位无符号数加法可能导致溢出, 如溢出, \(x +_{w}^{u} y = x + y - 2^{w}\)(溢出去除最高位).
• w位无符号数减法可能导致负值, 如为负值, 结果 = 结果 + 2^w
• w位有符号数加法或减法可能导致溢出, 溢出后\(+2^{w}\)(或\(-2^{w}\)), 使之落在\([-2^{w-1}, 2^{w-1}-1]\)的范围内(溢出去除最高位).

乘法

• w位无符号数和有符号数乘法, 按位相乘后, 保留结果为2w位, 去除高w位, 即为结果
• 由于乘法指令很慢(10个或更多时钟周期), 因此将乘数分解为多个2的次方的和, 将乘法转为移位操作, 提高运算速度

除法

• 无符号数相除, 使用长除法, 结果向下取整, 除不尽的余数舍弃.
• 有符号数相除, 除数为正数时, 使用长除法, 结果向下取整, 被除数为正数情况与无符号数相同, 被除数负数情况时, 需要加偏置(biasing).
• 除数为2的幂时, 为特殊情况, 可以用移位替代, 提高运算速度. 注意偏置.

浮点数

IEEE浮点数, \(V = (-1)^{s} * frac * 2 ^{exp}\)
单精度32位, s, exp, frac的位数为1, 8 , 23; 双精度64位, s, exp, frac的位数为1, 11, 52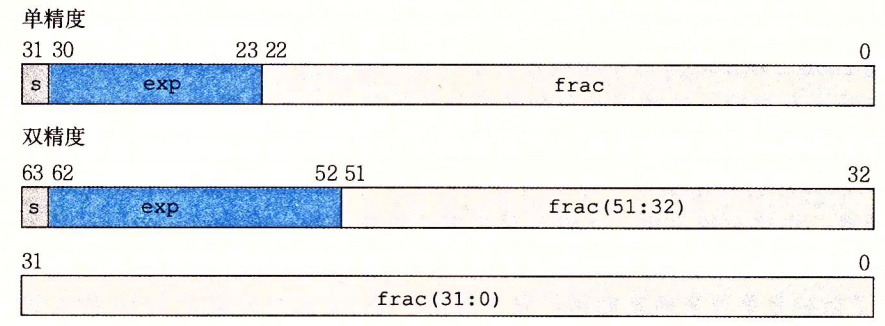

浮点数运算不满足交换律, 结合律, 分配律

转载于:https://www.cnblogs.com/winwink/p/CSAPP_Note_Chapter2_Bit_part2.html