leetcode_173【二叉搜索树迭代器】

最新推荐文章于 2024-03-09 17:27:57 发布

weixin_30315723

最新推荐文章于 2024-03-09 17:27:57 发布

阅读量60

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/chengsheng/p/10464891.html

本文介绍了一种实现二叉搜索树迭代器的方法，通过初始化左子节点入栈，next()方法返回下一个最小值，并将右子树的左节点入栈，hasNext()检查栈是否为空来判断是否有下一个元素。此实现保证了时间和空间复杂度为O(1)和O(h)。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

示例：

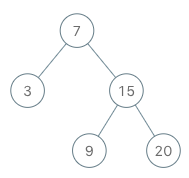
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

提示：

next() 和 hasNext() 操作的时间复杂度是 O(1)，并使用 O(h) 内存，其中 h 是树的高度。
你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) {
        //初始化所有左节点入栈
        for(; root != NULL; root = root->left){
            stk.push(root);
        }
    }

    /** @return the next smallest number */
    int next() {
        TreeNode* pnode = stk.top();
        stk.pop();
        int val = pnode->val;
        //换成右子树的根
        pnode = pnode->right;
        //右子树的所有左节点入栈
        for(; pnode != NULL; pnode = pnode->left){
            stk.push(pnode);
        }
        return val;
    }

    /** @return whether we have a next smallest number */
    bool hasNext() {
        return stk.empty()? false: true;
    }
private:
    stack<TreeNode*> stk;
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */

转载于:https://www.cnblogs.com/chengsheng/p/10464891.html