条件:
1、选定的V0节点
2、邻接矩阵
准备:
1、dist[n]数组:用于记录从V0到Vi的当前最短路径,初始值为邻接矩阵的第0行(也就是V0到各点的直接距离)
2、path[n]数组:用于记录V0到Vi的前一个节点,这样最后可以通过这个得出V0到每个节点的路径,初始值,如果dist[i]!=-1则为0,dist[i]==-1则为-1
算法思想:
1、设定当前定点集只有V0
2、从dist[n]中找到最短的一条路径,指向Vi
3、将Vi归入当前定点集合,并且更新dist[n]和path[n]
将V0直接到其他节点的长度,和V0通过Vi到其他节点的长度进行比较,如果发现后者更短,则
更新dist[n]修改为更短的距离
更新path[n],修改为Vi
大体上就是这样,不断将新的点纳入,不断更新路径,直到把所有点都纳入
最后附上一张图片,但愿看得懂=v=
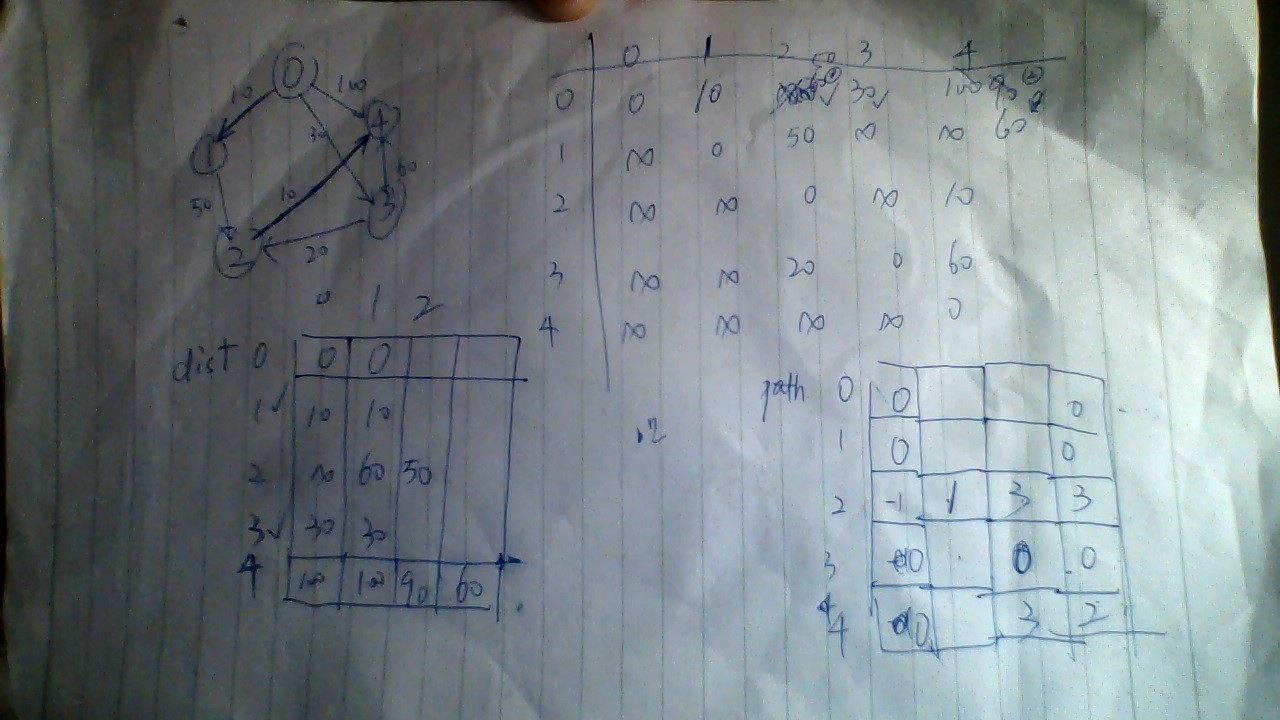







 本文详细介绍了一种寻找图中两点间最短路径的经典算法——Dijkstra算法。文章首先介绍了算法所需的条件与准备工作,包括选定起点V0及邻接矩阵等;然后逐步解析了算法的核心思想,即如何不断更新路径并纳入新的节点,最终实现从起始节点到其他所有节点的最短路径计算。
本文详细介绍了一种寻找图中两点间最短路径的经典算法——Dijkstra算法。文章首先介绍了算法所需的条件与准备工作,包括选定起点V0及邻接矩阵等;然后逐步解析了算法的核心思想,即如何不断更新路径并纳入新的节点,最终实现从起始节点到其他所有节点的最短路径计算。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








