《数据压缩》第五次作业

《数据压缩》作业五：

    教材 page 44

          3，9 ，12，15，16

3-3  证明：I(X;Y)=H(X)-H(X|Y)。

   证：

       

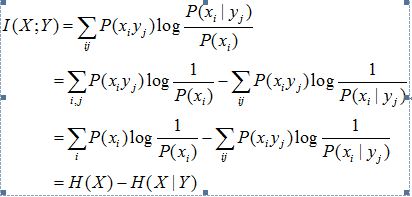
        根据上述，I(X;Y)=H(X)-H(X|Y)得证。

3-9  没有冗余度的信源还能不能压缩？为什么？

     答：不能进行无损压缩，但是可以进行有损压缩。

   因为无损压缩也叫做冗余度压缩，数据=信息+冗余度，是去除（至少是减少）那些可能是后来插入数据中的冗余度，所以没有冗余的信源是不能进行无损压缩的。
   有损压缩是将次要的信息数据压缩掉，牺牲一些质量来减少数据量，允许压缩过程中损失一定的的信息，虽然不能完全恢复原始数据，但是所损失的部分对理解原始图像的影响缩小，所以如果没要求较高的质量的话，有无冗余度是没有关系的，都是可以进行有损压缩的。

 

3-12 等概率分布的信源还能不能压缩？为什么？你能举例说明吗？

    答：至少是可以进行有损压缩的，另外，“等概”“未必”“不相关”，例如对方波信号或锯齿波信号的均匀取样值。如果信源是离散无记忆信源，那么信源符号是有一定的概率分布的，就可以进行无失真编码。但是只要信源不是等概率分布，就存在着数据压缩的可能性，所以至少是可以进行有损压缩的， 无损压缩就不一定了。

 

3-15 有人认为：“图像的负片（黑白颠倒）比正片更容易压缩”。你同意他的观点吗？为什么？

     答：我不同意他的观点。因为图像的负片（黑白颠倒）和正片两者相比较两者的熵是一样的，进行压缩是没有什么差异的，就算进行一阶熵、二阶熵和差分熵结果都是一样的。

 

3-16 有人认为：“相关的信源是非等概率分布的”。你同意他的观点吗？为什么？

   答：我不同意他的观点。因为只要信源不是等概率分布，就存在数据压缩的可能性，而且相关的信源是能进行压缩的，在进行无损压缩时就说明信源是有冗余度的，则该信源就是非等概率分布的，但是不代表相关的信源是非等概率分布的，这种说法不具体，比较片面。

 

转载于:https://www.cnblogs.com/py96/p/6100838.html