ML_KNN算法

算法步骤:

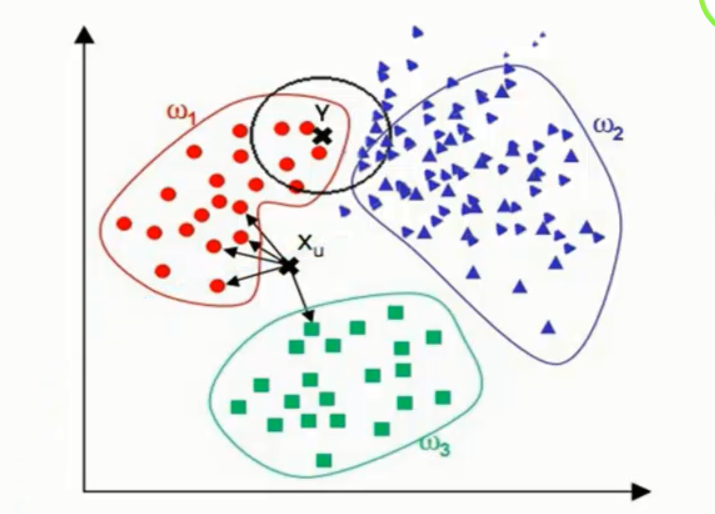
为了判断未知实例的类别，以所有已知类别的实例作为参照

选择参数K

计算未知实例与所有已知实例的距离

选择最近K个已知实例

根据少数服从多数的投票法则（majority-voting）,让未知实例归类为K个最邻近样本中最多数的类别

 

细节：

关于K

关于距离的衡量方法:

　　Euclidean Distance定义

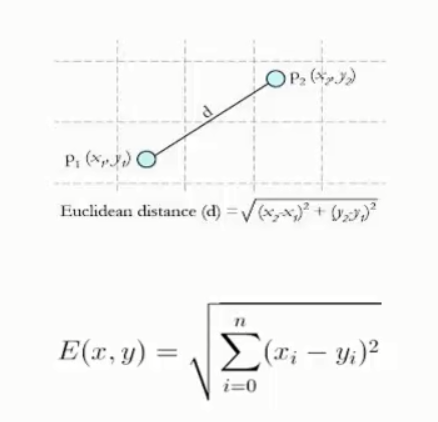
其他距离衡量:余弦值（cos）、相关度（correlation）、曼哈顿距离（Manhattan distance）

 

算法优缺点：

优点：

　　简单

　　易于理解

　　容易实现

　　通过对K的选择可具备丢噪音数据的健壮性

缺点：

　　

 

　　需要大量空间储存所有已知实例

　　算法复杂度高（需要比较所有已知实例与要分类的实例）

　　当其样本分布不平衡时，比如其中一类样本过大（实例数量过多）占主导的时候，新的未知实例容易被归类为这个主导样本，因为这类样本实例的数量过大，但这个新的未知实例实际并未接近目标样本

 

改进版本：

　　考虑距离，根据距离加上权重

　　比如：1/d(距离）

 

　　

 

转载于:https://www.cnblogs.com/wuweixiong/p/10432088.html