poj 1185 炮兵阵地状压dp

最新推荐文章于 2021-07-15 11:32:37 发布

weixin_30274627

最新推荐文章于 2021-07-15 11:32:37 发布

阅读量62

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/au-xiaotian/p/3457498.html

本文介绍了一种解决二维炮塔放置问题的动态规划算法。该算法通过深度优先搜索（DFS）预处理所有可能的炮塔放置状态，并利用三维动态规划（DP）表来找出最优解。具体来说，dp[i][r][p]表示第i行处于特定状态r和p时的最大炮塔数量。文章还提供了完整的C++代码实现。

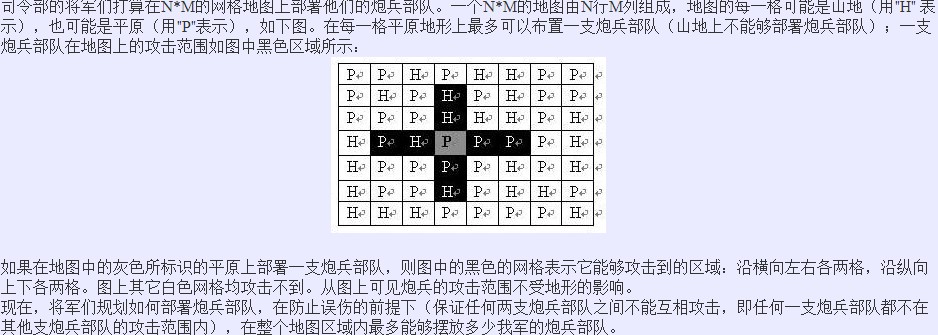
分析：因为每一行的状态和上两行的状态有关，因此dp[i][r][p]代表第i行状态为state[r]以及第i-1行为state[p]时的最大炮台数目；

状态是有限的，可以dfs出来

代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<deque>
//#define DEBUG  //todo
using namespace std;    int nn;
int ans;
int m,n,cnt,bin[11],dp[110][110][110],state[100],t,gra[110],_cnt,sum[110];
char c;
void ini()
{
    t=0;
    cnt=0;
    cin>>m>>n;
    for(int i=1;i<=m;i++){
        getchar();
        for(int j=1;j<=n;j++){
            cin>>c;
            if(c=='P') gra[i]+=1<<(n-j);
        }
    }
}
void dfs(int i)
{
    if(i>=n) {
        state[++cnt]=t; sum[cnt]=_cnt;
        return; }
    for(int j=i+1;;j++){
        if(j>n) { dfs(j); break;}
        if(j-i>=3 || i==0) { 
            t+=1<<(j-1);
            _cnt++;
            dfs(j);
            t-=1<<(j-1);
            _cnt--;
        }
    }
}
void work()
{
    dfs(0);
    memset(dp,-1,sizeof(dp));
    for(int p=1;p<=cnt;p++){
        for(int q=1;q<=cnt;q++){
            if((state[p]&gra[1])==state[p] && state[q]==0){
                dp[1][p][q]=sum[p];
            }
        }
    }
    for(int i=2;i<=m;i++){
        for(int r=1;r<=cnt;r++){
            if((gra[i]&state[r])!=state[r]) continue;
            for(int p=1;p<=cnt;p++){
                if((state[p]&state[r])!=0) continue;
                for(int q=1;q<=cnt;q++){
                    if(dp[i-1][p][q]==-1 || (state[r]&state[q])!=0) continue;
                    dp[i][r][p]=max(dp[i][r][p],dp[i-1][p][q]+sum[r]);
                }                
            }
        }
    }
    for(int r=1;r<=cnt;r++){
        for(int p=1;p<=cnt;p++){
            ans=max(dp[m][r][p],ans);
        }
    }
    cout<<ans<<endl;
}
int main()
{
    ini();
    work();
#ifdef DEBUG
    cin>>nn;
#endif
    return 0;
}
//dp[i][r][p]=max(dp[i-1][p][_p]+sum[r]);