【bzoj4010】[HNOI2015]菜肴制作 拓扑排序+堆
题目大意:求编号位置序最小(每个编号所在位置最小)
方法1:
建链表,每次把需要放在他前面的放前面,递归去找,最后的表应该就是答案,但是他好像是错的
30·


1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<iostream> 6 #include<cmath> 7 #include<queue> 8 using namespace std; 9 const int maxn=1e5+5; 10 int n,m,T; 11 int fst[maxn],nxt[maxn],to[maxn],edge_count,indegree[maxn]; 12 inline void add(int x,int y){ 13 edge_count++; 14 to[edge_count]=y; 15 nxt[edge_count]=fst[x]; 16 fst[x]=edge_count; 17 indegree[y]++; 18 } 19 bool vis[maxn]; 20 queue<int>q; 21 int cnt; 22 inline bool topological_sort(){ 23 cnt=0; 24 for(int i=1;i<=n;i++)if(!indegree[i])q.push(i),cnt++; 25 while(q.size()){ 26 int u=q.front(); 27 q.pop(); 28 29 for(int i=fst[u];i;i=nxt[i]){ 30 int v=to[i]; 31 indegree[v]--; 32 if(!indegree[v])q.push(v),cnt++; 33 } 34 } 35 return cnt==n; 36 } 37 int pre[maxn],suf[maxn]; 38 inline void ins(int x,int p){//在p( 数值 )前插入x 39 int l=pre[p]; 40 pre[x]=l; 41 suf[l]=x; 42 43 pre[p]=x; 44 suf[x]=p; 45 46 vis[x]=1; 47 } 48 inline void del(int x){//将x从链表中删除 49 int l=pre[x]; 50 int r=suf[x]; 51 suf[l]=r; 52 pre[r]=l; 53 } 54 inline void init(){ 55 for(int i=0;i<=n+1;i++){ 56 pre[i]=i-1; 57 suf[i]=i+1; 58 } 59 } 60 int flag[maxn]; 61 int temp[maxn],p; 62 inline void solve(int x,int y){//传数值 63 int dep=++cnt; 64 for(int k=x;pre[k]!=y;k=suf[k])flag[k]=dep; 65 66 for(int k=x;flag[k]==dep;k=suf[k]){ 67 p=0; 68 vis[k]=1; 69 70 for(int i=fst[k];i;i=nxt[i]){ 71 int v=to[i]; 72 if(!vis[v])temp[++p]=v; 73 } 74 if(p){ 75 sort(temp+1,temp+p+1); 76 for(int i=1;i<=p;i++){ 77 del(temp[i]); 78 ins(temp[i],k); 79 } 80 solve(temp[1],temp[p]); 81 } 82 } 83 if(x==1 && y==n){ 84 for(int k=1,ans=1;ans<=n;k=suf[k],ans++){ 85 printf("%d ",k); 86 } 87 printf("\n"); 88 } 89 } 90 inline void clear(){ 91 memset(indegree,0,sizeof(indegree)); 92 memset(fst,0,sizeof(fst)); 93 memset(nxt,0,sizeof(nxt)); 94 memset(to,0,sizeof(to)); 95 edge_count=0; 96 memset(vis,0,sizeof(vis));//标记是否处理过 97 memset(pre,0,sizeof(pre)); 98 memset(suf,0,sizeof(suf)); 99 init(); 100 } 101 int main(){ 102 103 scanf("%d",&T); 104 while(T--){ 105 106 scanf("%d%d",&n,&m); 107 clear(); 108 for(int i=1,a,b;i<=m;i++){ 109 scanf("%d%d",&a,&b); 110 add(b,a);//b前面有a 111 } 112 if(!topological_sort()){printf("impossible\n");continue;} 113 else cnt=0,solve(1,n); 114 } 115 return 0; 116 }
希望dalao们想出反例...
。。。艹。。。Rechardluan竟然在几分钟之内就想到反例了
我的算法是基于保证比x小的节点都在x前面,但是问题就在于 每次处理的序列并不一定符合题目要求(不完全等价),比如一组数据是
5 3
5 2
4 2
3 5
12345 -> 1 45 23 -> 14 3 52
但是正确答案应该是
13452
正解:
一个数的位置确定,当且仅当比这个数大的 以及 必须在他后面的 都在他后面(不能把 比他小的放前面,会有问题)
所以我们会想到建反图,每次找最大的 零度节点 删除
最后倒序输出就是答案,完美的避开了之前说的递归区间会有的问题
std:


1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<iostream> 6 #include<cmath> 7 #include<queue> 8 using namespace std; 9 const int maxn=1e5+5; 10 int n,m,T; 11 int fst[maxn],nxt[maxn],to[maxn],edge_count,indegree[maxn]; 12 inline void add(int x,int y){ 13 edge_count++; 14 to[edge_count]=y; 15 nxt[edge_count]=fst[x]; 16 fst[x]=edge_count; 17 indegree[y]++; 18 } 19 bool vis[maxn]; 20 priority_queue<int>q; 21 int ans[maxn]; 22 int cnt; 23 inline bool topological_sort(){ 24 cnt=0; 25 for(int i=1;i<=n;i++)if(!indegree[i]){ 26 q.push(i); 27 } 28 while(q.size()){ 29 int u=q.top(); 30 ans[++cnt]=u; 31 q.pop(); 32 33 for(int i=fst[u];i;i=nxt[i]){ 34 int v=to[i]; 35 indegree[v]--; 36 if(!indegree[v])q.push(v); 37 } 38 } 39 return cnt==n; 40 } 41 inline void clear(){ 42 memset(indegree,0,sizeof(indegree)); 43 memset(fst,0,sizeof(fst)); 44 memset(nxt,0,sizeof(nxt)); 45 memset(to,0,sizeof(to)); 46 edge_count=0; 47 } 48 int main(){ 49 scanf("%d",&T); 50 while(T--){ 51 scanf("%d%d",&n,&m); 52 clear(); 53 for(int i=1,a,b;i<=m;i++){ 54 scanf("%d%d",&a,&b); 55 add(b,a);//b前面有a 56 } 57 if(!topological_sort()){printf("impossible\n");continue;} 58 else{ 59 for(int i=n;i;i--){ 60 printf("%d ",ans[i]); 61 } 62 printf("\n"); 63 } 64 } 65 return 0; 66 }
总结:
1.证明算法的复杂度。2.证明算法的正确性(往往贪心算法都需要想反例,从算法的 每一步 去思考,想出可能会造成问题的环节)
bzoj3329 Xorequ 【数位DP+Fibonacci】
求满足所有1<=i<=n的i s.t. i ^ (2 * i)==i + (2*i)的i的个数
n<=1e(10^18)
求二进制下没有相邻的1的数的个数
本题写的非常曲折,本来想就是一个数位Dp,但是小于等于n的问题不太好解决,根据原则:不会做DP就再加一维
又添加了一维表示比当前大还是比当前小,后来成功的谢了16个特判A了,但是后来仔细想想,只需要预处理Fibonacci数列,二进制下每次遇到1都加上Fibonacci
就可以很简单的AC了
std:


1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #define LL long long 6 using namespace std; 7 long long f[100][2][2]; 8 int T; 9 long long n; 10 //[0]比原来小,[1]比原来大 11 //[0]选0,[1]选1 12 int main(){ 13 //freopen("3.out","w",stdout); 14 //scanf("%d",&T); 15 scanf("%d",&T); 16 17 while(T--){ 18 scanf("%lld",&n); 19 20 memset(f,0,sizeof(f)); 21 if(n&1ll){ 22 f[0][0][0]=1ll; 23 f[0][0][1]=0ll; 24 f[0][1][0]=1ll; 25 f[0][1][1]=0ll; 26 } 27 else{ 28 f[0][0][0]=1ll; 29 f[0][0][1]=0ll; 30 f[0][1][0]=0ll; 31 f[0][1][1]=1ll; 32 } 33 LL i; 34 for(i=1ll;(1ll<<i)<=n;i++){ 35 if(!(n&(1ll<<i)) && !(n&(1ll<<(i-1ll) ) ) ){//00 36 //cout<<1; 37 f[i][0][0]=f[i-1][0][0]; 38 f[i][0][1]=f[i-1][1][0]+f[i-1][1][1]+f[i-1][0][1]; 39 f[i][1][0]=0ll; 40 f[i][1][1]=f[i-1][0][1]+f[i-1][0][0]; 41 } 42 else if(!(n&(1ll<<i)) && (n&(1ll<<(i-1ll) ) ) ){//01 43 // cout<<2; 44 f[i][0][0]=f[i-1][1][0]+f[i-1][0][1]+f[i-1][0][0]; 45 f[i][0][1]=f[i-1][1][1]; 46 f[i][1][0]=0ll; 47 f[i][1][1]=f[i-1][0][1]+f[i-1][0][0]; 48 } 49 else if((n&(1ll<<i)) && !(n&(1ll<<(i-1ll) ) ) ){//10 50 //cout<<3; 51 f[i][0][0]=f[i-1][1][0]+f[i-1][1][1]+f[i-1][0][1]+f[i-1][0][0]; 52 f[i][0][1]=0ll; 53 f[i][1][0]=f[i-1][0][0]; 54 f[i][1][1]=f[i-1][0][1]; 55 } 56 else{//11 57 //cout<<4; 58 f[i][0][0]=f[i-1][1][0]+f[i-1][1][1]+f[i-1][0][1]+f[i-1][0][0]; 59 f[i][0][1]=0ll; 60 f[i][1][0]=f[i-1][0][1]+f[i-1][0][0]; 61 f[i][1][1]=0ll; 62 } 63 //printf("less%d %d bigger%d %d\n",f[i][1][0],f[i][0][0],f[i][0][1],f[i][1][1]); 64 } 65 printf("%lld\n",f[i-1][1][0]+f[i-1][0][0]-1ll);//去掉0 66 } 67 return 0; 68 }
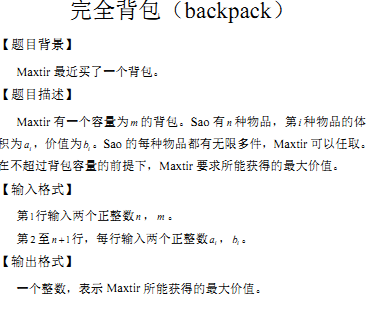

体积巨大的完全背包【数学+背包】
n<=1e5,m<=1e18,1<=ai<=100
这道题显然要从ai的大小入手,考虑到ai 很小,我们对于1~100之间求出同体积的最大价值
然后证明一个引理??
引理:给定任意个整数(不一定不同),它们之中存在若干个整数的和为n的倍数。
证明:设n个整数为a1~an
S1~Sn 为前缀和
对于S0~Sn这n+1个数,至少有两个数模相同,则这两个数的差为的倍数,证毕。
设:S为性价比最高且体积最小的物品,x为最优情况下除S外的其他物品个数
定理:存在一种最优情况使得x< S的体积(a[s])。
证明:若x> a[s],则存在若干件物品的和为 a[s] 的倍数,将这些物品用第种物品替换一定不劣。
于是这件非第s种物品的和最大为100*a[s]。于是我们选择(n/a[x]-100)件第s种物品,剩下的空间做完全背包,复杂度O(n^3)。
force(but ac):


1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<ctime> 8 #define LL long long 9 using namespace std; 10 const int maxn=1e6+5; 11 const int maxit=1e2+5; 12 const LL INF=1ll<<62; 13 int cnt; 14 struct item{ 15 int w;//体积 16 int v;//价值 17 const bool operator<(const item & x)const { 18 return 1.0*v/w > 1.0*x.v/x.w; 19 } 20 }it[maxit]; 21 int n,a[maxn],b[maxn]; 22 int Maxvalue[maxit]; 23 LL f[maxn]; 24 LL m; 25 26 inline void force1(){ 27 for(int i=1;i<=n;i++)scanf("%d%d",&a[i],&b[i]); 28 for(int i=1;i<=m;i++){ 29 f[i]=-INF; 30 } 31 for(int i=1;i<=n;i++){ 32 for(int j=a[i];j<=m;j++){ 33 f[j]=max(max(f[j],f[j-1]),f[j-a[i]]+b[i]); 34 } 35 } 36 printf("%lld\n",f[m]); 37 exit(0); 38 } 39 inline void force2(){ 40 //cout<<"enter2"<<endl; 41 for(int i=1;i<=n;i++){ 42 scanf("%d%d",&a[i],&b[i]); 43 Maxvalue[ a[i] ]=max(Maxvalue[ a[i] ],b[i]);//相同体积价值最大化 44 } 45 //for(int i=1;i<=100;i++)printf("%d:%d\n",i,Maxvalue[i]); 46 for(int i=1;i<=m;i++){ 47 f[i]=-INF; 48 } 49 for(int i=1;i<=m;i++){ 50 for(int j=1;j<=100;j++){ 51 if(i>=j)f[i]=max(f[i],f[i-j]+Maxvalue[j]); 52 } 53 } 54 printf("%lld\n",f[m]); 55 exit(0); 56 } 57 inline void ac(){ 58 LL ans=0ll; 59 for(int i=1;i<=n;i++){ 60 scanf("%d%d",&a[i],&b[i]); 61 Maxvalue[ a[i] ]=max(Maxvalue[ a[i] ],b[i]);//相同体积价值最大化 62 } 63 for(int i=1;i<=maxit-5;i++){ 64 if(Maxvalue[i]){ 65 it[++cnt].w=i; 66 it[cnt].v=Maxvalue[i]; 67 } 68 } 69 70 sort(it+1,it+cnt+1);//斜率排序 71 for(int i=1;i<=100000;i++){//预处理 72 f[i]=-INF; 73 } 74 for(int i=1;i<=100000;i++){ 75 for(int j=1;j<=100;j++){ 76 if(i>=j)f[i]=max(f[i],f[i-j]+Maxvalue[j]); 77 } 78 } 79 ans=m/it[1].w*it[1].v+f[m%it[1].w]; 80 for(LL i=1;i<=100000;i++){ 81 //if(m==i)cout<<"shit"<<endl; 82 ans=max((LL)((m-i)/(it[1].w))*it[1].v+f[i+(m-i)%it[1].w],max(ans,(LL)(m/i)*f[i]+f[m%i])); 83 } 84 printf("%lld\n",ans); 85 } 86 int main(){ 87 //freopen("backpack3.in","r",stdin); 88 srand(time(0)); 89 90 scanf("%d%lld",&n,&m); 91 if(n<=1000&&m<=1000)force1(); 92 else if(m<=100000)force2(); 93 else ac(); 94 //else printf("%d",rand()); 95 return 0; 96 }
总结:
1.数据范围极大时 寻找突破口,往往会有一些小性质应该先证明出来
2.无法证明时尽量想暴力+优化,正解往往不好想
3.平时做题应该多思考思考数据范围大了该咋办
————————线段树shit题集锦————————
T1



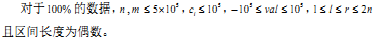
本题极其无聊,3T强行捏成1T,差最大 显然是 前一半后一半,差最小显然是间隔着放,方案数显然是卡特兰数列
关于卡特兰数列,直接放公式了h(n)=C(2n,n)/(n+1) (n=0,1,2,...) or h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
也就是2n 个数0 1,保证在任何位置都有:之前的1的个数<= 0的个数 之类的问题
维护:
1.求和数组,每次右半边的和 - 左半边的和
2.奇正偶负数组,每次询问时判断L是奇是偶在考虑正负
3.组合数


1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<iostream> 5 #include<cstdlib> 6 #include<cmath> 7 #define LL long long 8 using namespace std; 9 const LL P=1e9+7; 10 /* 11 数据结构??? 12 两个线段树,katalan数列 13 */ 14 15 const int maxn=2e6+5; 16 int n,m,c[maxn],opt,l,r; 17 LL val; 18 int sum[maxn<<2][2],lazy[maxn<<2]; 19 inline void update(int k){ 20 sum[k][0]=(1ll*sum[k<<1][0]+sum[k<<1|1][0])%P; 21 sum[k][1]=(1ll*sum[k<<1][1]+sum[k<<1|1][1])%P; 22 } 23 inline void change(int k,int l,int r,LL x){ 24 sum[k][0]=(1ll*sum[k][0]+x*(r-l+1))%P;//和 25 lazy[k]=(1ll*lazy[k]+x)%P; 26 27 if((r-l)&1)return;//差 28 else{ 29 sum[k][1]=(1ll*sum[k][1]+((l&1)?x:-x))%P; 30 } 31 } 32 void build(int k,int l,int r){ 33 if(l==r){ 34 //差数列 2n+1 + 2n - 35 sum[k][1]=( (l&1) ? c[l] : -c[l] ); 36 //和数列 37 sum[k][0]=c[l]; 38 39 return; 40 } 41 else{ 42 int mid=(l+r)>>1; 43 build(k<<1,l,mid); 44 build(k<<1|1,mid+1,r); 45 update(k); 46 } 47 } 48 inline void down(int k,int l,int r){ 49 if(lazy[k]){ 50 int mid=(l+r)>>1; 51 change(k<<1,l,mid,1ll*lazy[k]); 52 change(k<<1|1,mid+1,r,1ll*lazy[k]); 53 lazy[k]=0ll; 54 } 55 } 56 void modify(int k,int l,int r,int x,int y,LL xx){ 57 if(l>r){cout<<"shit";exit(0);} 58 59 if(x<=l && r<=y){ 60 change(k,l,r,xx); 61 return; 62 } 63 else{ 64 down(k,l,r); 65 66 int mid=(l+r)>>1; 67 if(x<=mid)modify(k<<1,l,mid,x,y,xx); 68 if(mid<y)modify(k<<1|1,mid+1,r,x,y,xx); 69 update(k); 70 } 71 } 72 int query(int k,int l,int r,int x,int y,int b){ 73 if(l>r){cout<<"shit";exit(0);} 74 75 if(x<=l&&r<=y){ 76 return sum[k][b]%P; 77 } 78 else{ 79 down(k,l,r); 80 81 int ans=0ll; 82 int mid=(l+r)>>1; 83 if(x<=mid)ans=(1ll*ans+query(k<<1,l,mid,x,y,b))%P; 84 if(mid<y)ans=(1ll*ans+query(k<<1|1,mid+1,r,x,y,b))%P; 85 86 return ans; 87 } 88 } 89 LL jc[maxn],njc[maxn],inv[maxn]; 90 inline void com_init(){ 91 jc[0]=njc[0]=jc[1]=njc[1]=inv[1]=1ll; 92 for(LL i=2ll;i<=(n<<1);i++){ 93 jc[i]=jc[i-1]*i%P; 94 inv[i]=(P-P/i)*inv[P%i]%P; 95 njc[i]=njc[i-1]*inv[i]%P; 96 } 97 } 98 inline LL C(int n,int m){//组合数注意边界问题 99 100 return jc[n]*njc[n-m]%P*njc[m]; 101 } 102 int main(){ 103 scanf("%d%d",&n,&m); 104 //if(m<=100)cout<<n<<" "<<m<<endl; 105 for(int i=1;i<=(n<<1);i++){ 106 scanf("%d",&c[i]); 107 //if(m<=100)cout<<c[i]<<" "; 108 } 109 110 com_init(); 111 build(1,1,n<<1); 112 113 for(int i=1;i<=m;i++){ 114 scanf("%d",&opt); 115 //if(m<=100)cout<<opt<<" "; 116 if(opt){ 117 scanf("%d%d",&l,&r); 118 //if(m<=100)cout<<l<<" "<<r<<endl; 119 int mid=(l+r)>>1; 120 int len=r-l+1; 121 122 printf("%d %d %lld\n",-query(1,1,n<<1,l,mid,0)+query(1,1,n<<1,mid+1,r,0),((l&1)?-query(1,1,n<<1,l,r,1):query(1,1,n<<1,l,r,1)),( ( C(len,len>>1)-C(len,(len>>1)-1) )%P+P)%P ); 123 } 124 else{ 125 126 scanf("%d%d%lld",&l,&r,&val); 127 //if(m<=100)cout<<l<<" "<<r<<" "<<val<<endl; 128 modify(1,1,n<<1,l,r,val); 129 } 130 } 131 return 0; 132 } 133 /* 134 10 10 135 0 2 10 18 19 27 27 35 35 45 46 53 56 59 67 70 75 93 93 100 1 136 0 5 10 0 137 0 6 11 7 138 0 6 7 -14 139 0 10 13 3 140 0 3 20 -4 141 0 9 16 4 142 1 16 17 143 1 5 6 144 0 5 14 7 145 146 41 13 5 147 1 1 1 148 1 1 1 149 */
...考试时空间炸了,so segment_tree在写的时候尽量不把废物信息(左右端点)存起来,尽量在递归里面写
T2



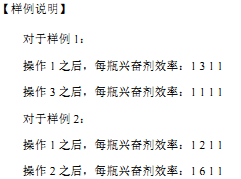

线段树维护乘积+逆元(注意long long,注意空间别爆了)


1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<cmath> 5 #include<algorithm> 6 #include<iostream> 7 #define LL long long 8 using namespace std; 9 const int maxn=1e6+5; 10 const LL P=1e9+7; 11 LL x,y; 12 void exgcd(LL a,LL b){//ax+by=1 13 if(!b){ 14 x=1ll;y=0;return; 15 } 16 exgcd(b,a%b); 17 18 LL t=y; 19 y=x-(a/b)*y; 20 x=t; 21 } 22 inline LL get_inv(LL a){ 23 exgcd(a,P); 24 //cout<<a<<" "<<x<<endl; 25 return (x%P+P)%P; 26 } 27 int root,lson[maxn<<2],rson[maxn<<2],cnt; 28 LL pi[maxn<<2]; 29 void modify(int &k,int l,int r,int p,int x,int b){ 30 if(!k){ 31 k=++cnt; 32 pi[k]=1ll; 33 } 34 35 if(l==r){ 36 pi[k]=((b==1)?(pi[k]*x%P):(pi[k]*get_inv((LL)x)%P)) ; 37 return; 38 } 39 int mid=(l+r)>>1; 40 if(p<=mid)modify(lson[k],l,mid,p,x,b); 41 else modify(rson[k],mid+1,r,p,x,b); 42 43 if(lson[k]&&rson[k])pi[k]=pi[lson[k]]*pi[rson[k]]%P; 44 else if(lson[k])pi[k]=pi[lson[k]]; 45 else if(rson[k])pi[k]=pi[rson[k]]; 46 } 47 LL query(int k,int l,int r,int x,int y){ 48 if(!k)return 1ll; 49 if(x<=l && r<=y)return pi[k];//线段树敲错了555 50 51 int mid=(l+r)>>1; 52 LL ans=1ll; 53 if(x<=mid)ans=ans*query(lson[k],l,mid,x,y)%P; 54 if(mid<y)ans=ans*query(rson[k],mid+1,r,x,y)%P;//线段树写反了 55 return ans; 56 } 57 int n,m; 58 int main(){ 59 //freopen("1.in","r",stdin); 60 61 scanf("%d%d",&n,&m); 62 int x,y,z; 63 cnt=1;//之前改过了以为之后也改了 64 pi[0]=pi[1]=1ll; 65 for(int i=1;i<=m;i++){ 66 scanf("%d%d%d",&x,&y,&z); 67 if(x==3){ 68 root=1; 69 printf("%lld\n",query(root,1,n,y,z)); 70 } 71 else{ 72 root=1; 73 modify(root,1,n,y,z,x); 74 } 75 } 76 return 0; 77 }
T3




线段树+状压:
每次正常修改,用int表示该区域有那些炮弹,区间合并就是 或 运算


1 #include<bits/stdc++.h> 2 #define Num(i) (1<<(i-1)) 3 using namespace std; 4 5 const int maxn=1e5+5; 6 int l,t,o; 7 inline int get_two(int x){ 8 int ans=0; 9 while(x){ 10 if(x&1)ans++; 11 x>>=1; 12 } 13 return ans; 14 } 15 int sum[maxn<<2],lazy[maxn<<2]; 16 inline void update(int k){ 17 sum[k]=sum[k<<1]|sum[k<<1|1]; 18 } 19 inline void change(int k,int t){ 20 sum[k]=Num(t); 21 lazy[k]=t; 22 } 23 inline void down(int k){ 24 if(lazy[k]){ 25 change(k<<1,lazy[k]); 26 change(k<<1|1,lazy[k]); 27 lazy[k]=0; 28 } 29 } 30 void build(int k,int l,int r){ 31 if(l==r){ 32 change(k,1); 33 return; 34 } 35 else{ 36 int mid=(l+r)>>1; 37 build(k<<1,l,mid); 38 build(k<<1|1,mid+1,r); 39 40 update(k); 41 //printf("l%d r%d sum%d\n",l,r,sum[k]); 42 } 43 } 44 void modify(int k,int l,int r,int x,int y,int t){ 45 if(x<=l&&r<=y){ 46 change(k,t); 47 return; 48 } 49 else{ 50 down(k); 51 52 int mid=(l+r)>>1; 53 54 if(x<=mid)modify(k<<1,l,mid,x,y,t); 55 if(mid<y)modify(k<<1|1,mid+1,r,x,y,t); 56 57 update(k); 58 } 59 } 60 inline int query(int k,int l,int r,int x,int y){ 61 if(x<=l&&r<=y){ 62 return sum[k]; 63 } 64 else{ 65 down(k); 66 67 int ans=0; 68 69 int mid=(l+r)>>1; 70 if(x<=mid)ans|=query(k<<1,l,mid,x,y); 71 if(mid<y)ans|=query(k<<1|1,mid+1,r,x,y); 72 73 return ans; 74 } 75 } 76 char ch[5]; 77 int main(){ 78 scanf("%d%d%d",&l,&t,&o); 79 build(1,1,l); 80 for(int i=1,a,b,c;i<=o;i++){ 81 scanf("%s",ch); 82 if(ch[0]=='C'){ 83 scanf("%d%d%d",&a,&b,&c); 84 if(a>b)swap(a,b); 85 modify(1,1,l,a,b,c); 86 } 87 else{ 88 scanf("%d%d",&a,&b); 89 if(a>b)swap(a,b); 90 printf("%d\n",query(1,1,l,a,b)); 91 } 92 } 93 return 0; 94 }

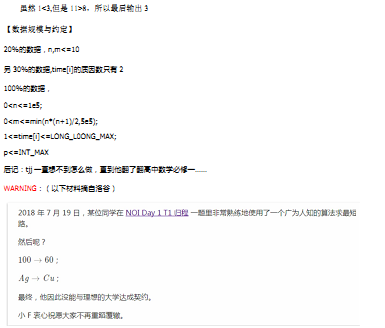
一道思路挺奇特的题,dijkstra算法是广为人知的最短路算法,但是不能求解带负环的,(同样的,乘法也可以,但是不能有除法环)
所以面对乘数极大的情况时,就要使用(double)log10()函数减少储存的数的大小,


1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdlib> 6 #include<cmath> 7 #include<queue> 8 #define LL long long 9 using namespace std; 10 template<typename T> 11 inline void read(T &a){ 12 a=0;T b=1;char x=getchar(); 13 while(x<'0'||'9'<x){ 14 if(x=='-')b=-1; 15 x=getchar(); 16 } 17 while('0'<=x&&x<='9'){ 18 a=(a<<1)+(a<<3)+x-'0'; 19 x=getchar(); 20 } 21 a*=b; 22 } 23 char C_[50]; 24 int TEMP; 25 template<typename T> 26 inline void write(T a){ 27 if(a<0){ 28 putchar('-'); 29 a=-a; 30 } 31 do{ 32 C_[++TEMP]=a%10+'0'; 33 a/=10; 34 }while(a); 35 while(TEMP)putchar(C_[TEMP--]); 36 } 37 const int maxn=1e5+5; 38 const int maxm=5e5+5; 39 40 int s,t,n,m; 41 LL p; 42 43 int fst[maxn],nxt[maxm<<1],to[maxm<<1],edge_count; 44 LL w[maxm<<1]; 45 double l[maxm<<1]; 46 inline void add(int x,int y,LL z){ 47 edge_count++; 48 to[edge_count]=y; 49 50 l[edge_count]=log10(z); 51 /*dijkstra算法乘法(没有除法)也能用; 52 但是受到无法记录路径长 的限制; 53 这时候就需要使用log函数,*变+ ; 54 从而让整个长度变得可以储存 55 */ 56 w[edge_count]=z%p; 57 nxt[edge_count]=fst[x]; 58 fst[x]=edge_count; 59 } 60 priority_queue<pair<double,int > >q; 61 bool vis[maxn]; 62 double dis[maxn]; 63 LL d[maxn]; 64 65 inline void dijkstra(){ 66 for(int i=1;i<=n;i++)dis[i]=100000000.0; 67 dis[s]=0.0;d[s]=1ll; 68 69 q.push(make_pair(-dis[s],s)); 70 while(q.size()){ 71 int u=q.top().second; 72 q.pop(); 73 if(vis[u])continue; 74 75 vis[u]=1; 76 for(int i=fst[u];i;i=nxt[i]){ 77 int v=to[i]; 78 double t=dis[u]+l[i]; 79 80 if(t<dis[v]){ 81 d[v]=d[u]*w[i]%p; 82 dis[v]=t; 83 q.push(make_pair(-dis[v],v)); 84 } 85 } 86 } 87 printf("%lld",d[t]); 88 } 89 int main() 90 { 91 scanf("%d%d%d%d%lld",&n,&m,&s,&t,&p); 92 int a,b;LL c; 93 for(int i=1;i<=m;i++){ 94 scanf("%d%d%lld",&a,&b,&c); 95 add(a,b,c);add(b,a,c); 96 } 97 dijkstra(); 98 return 0; 99 }
——————————矩阵加速递推shit题集锦——————————

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








