poj Connected Graph

最新推荐文章于 2021-09-23 19:31:28 发布

转载最新推荐文章于 2021-09-23 19:31:28 发布 · 124 阅读

1 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/one--world--one--dream/archive/2011/11/05/2237011.html

文章标签：

#java

这篇博客介绍了如何通过公式计算具有特定节点数的不同连通无向图的数量，详细解释了公式推导及应用过程，并提供了一个Java实现的示例代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Connected Graph

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 2197		Accepted: 1071

Description

An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
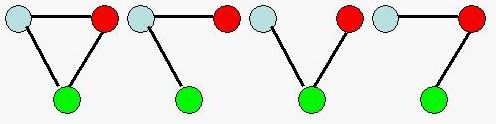
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.

Input

The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.

Output

For each test case output the answer on a single line.

Sample Input

Sample Output

Source

LouTiancheng@POJ

这是传说中的楼教主出的题，果然不一般呀；看的别人的题解呀，用java写的，牛呀

公式是f[n]=f[k]*f[n-k]*c[n-2][k-1]*((2^k)-1) (c[n-2][k]表示组合数,1<=k<n);考虑一个完整的联通图，可以标记两个点1，2。将点1，点2分别划分在两个子联通图中分别为g1，g2。在g1中最少要有一个点与g2中的点链接。这样的方式共2^k-1中，而g1总有c[n-2][k-1]个。将他们乘在一起就有了上面的式子(转载)。

import java.io.*;
import java.math.*;
import java.util.*;
public classMain{
static BigInteger p=BigInteger.valueOf(2);
public static void main(String[] args)
{
  Scanner cin=new Scanner(System.in);
int i,j,k;
     BigInteger c[][]=new BigInteger[52][52];
     BigInteger f[]=new BigInteger [52];
for(i=0;i<=50;i++)
     c[i][0]=c[i][i]=BigInteger.ONE;
for(i=1;i<=50;i++)
for(j=1;j<i;j++)
        c[i][j]=c[i-1][j-1].add(c[i-1][j]);

int n;

     f[1]=BigInteger.ONE;
     f[2]=BigInteger.ONE;
     f[3]=BigInteger.valueOf(4);
for(i=4;i<=50;i++)
{
      f[i]=BigInteger.ZERO;
for(k=1;k<i;k++)
{
       BigInteger t=BigInteger.ZERO;
       t=f[k].multiply(f[i-k]).multiply(c[i-2][k-1]);
       t=t.multiply(p.pow(k).subtract(BigInteger.ONE));
       f[i]=f[i].add(t);
}
}
while(cin.hasNext())
{
      n=cin.nextInt();
if(n==0)
break;
if(n==1||n==2)
{
       System.out.println(1);
continue;
}
         System.out.println(f[n]);
}
}
}