主成分分析

 

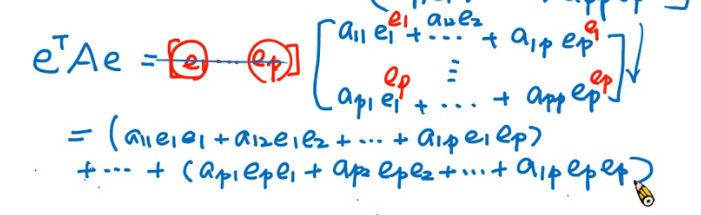
多元函数求导

 

 

 

 

 

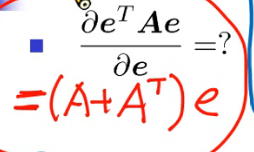
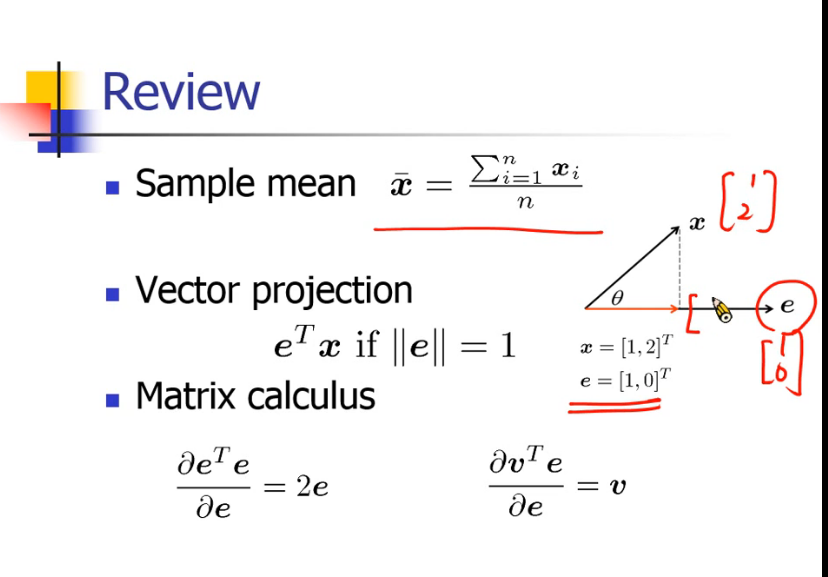
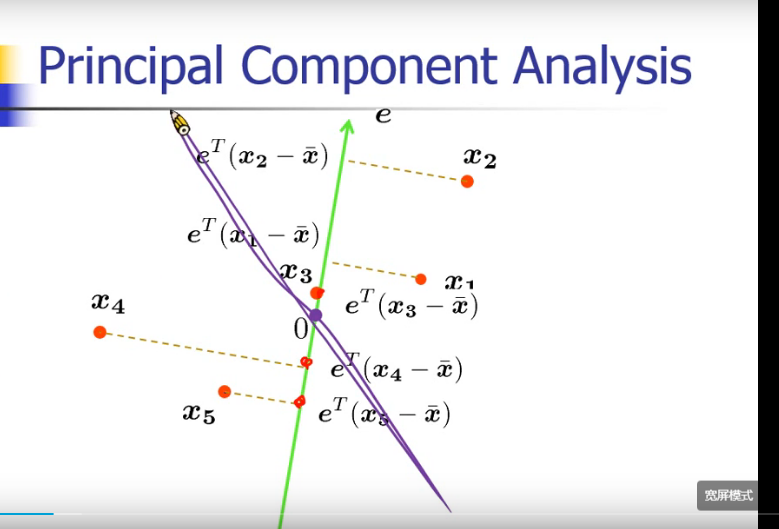
不同投影的距离不一样

pca 是要投影到最大的那一个

投影完了之后求和 再除以样本点的个数就是方差

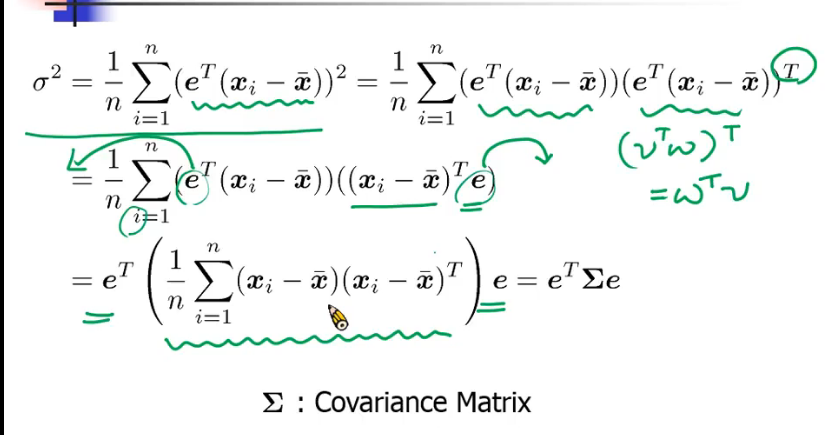
展开方差就是协方差，想找到e 使得 σ^2 最大

 

 

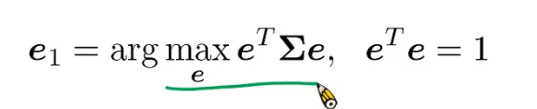存在某一个e使得 e1最大  

用拉格朗日条件法 来 求极值， 

构造函数：= 用原来的函数+λ乘限制条件

 

 

 

 

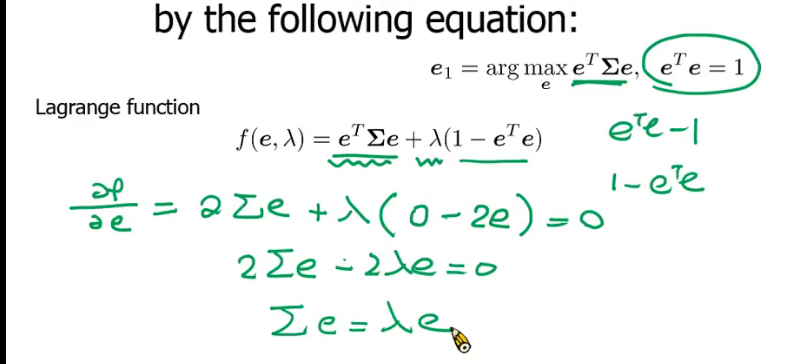
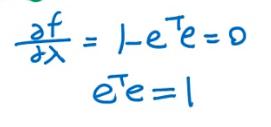
y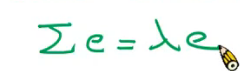两边同乘e的转置

 

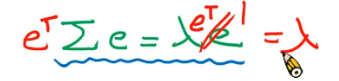
  由此发现 ，对比方差σ^2 定义   发现    特征值居然就是投影后的方差

 我要方差最大 就是求方差最大。第一主成分，就是特征值最大的那个

 

举一个例子

 

 

 

 

 

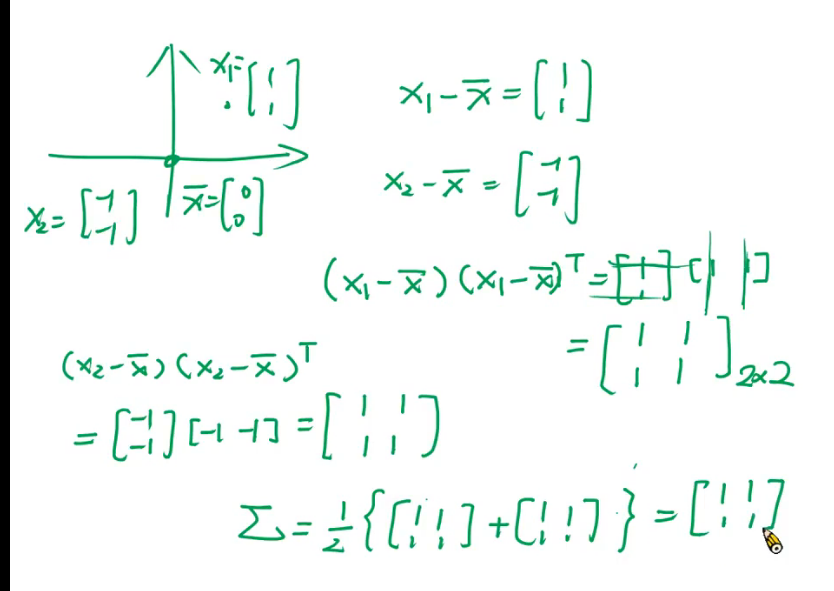
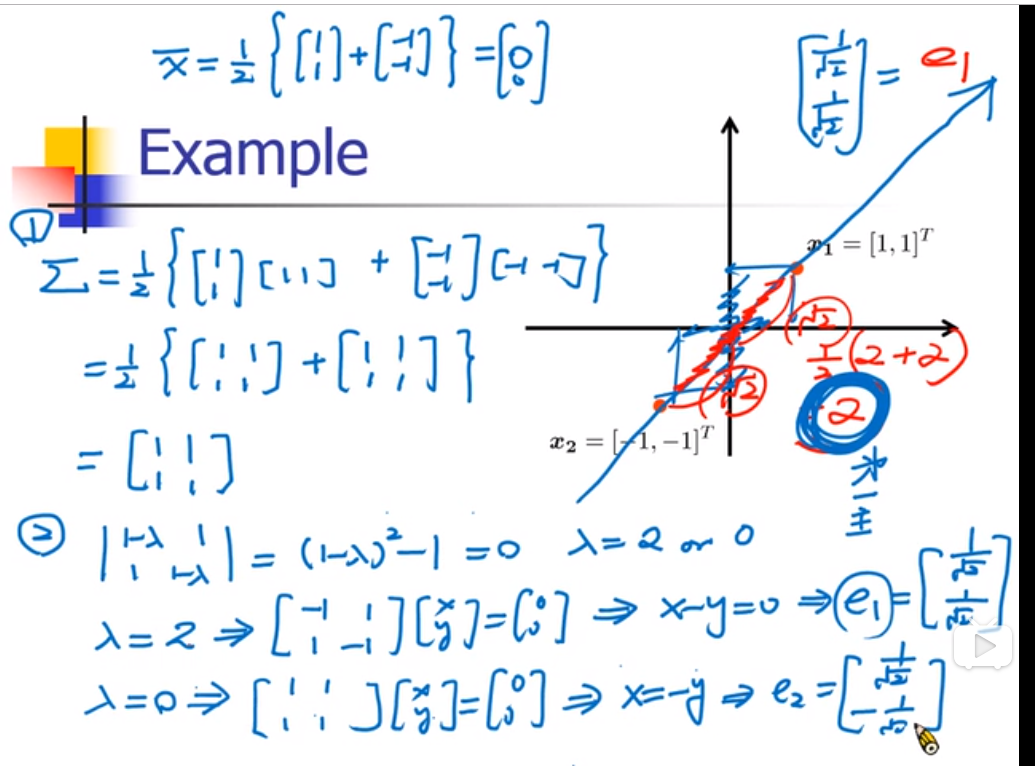
新的点加入 

 

 

 

 

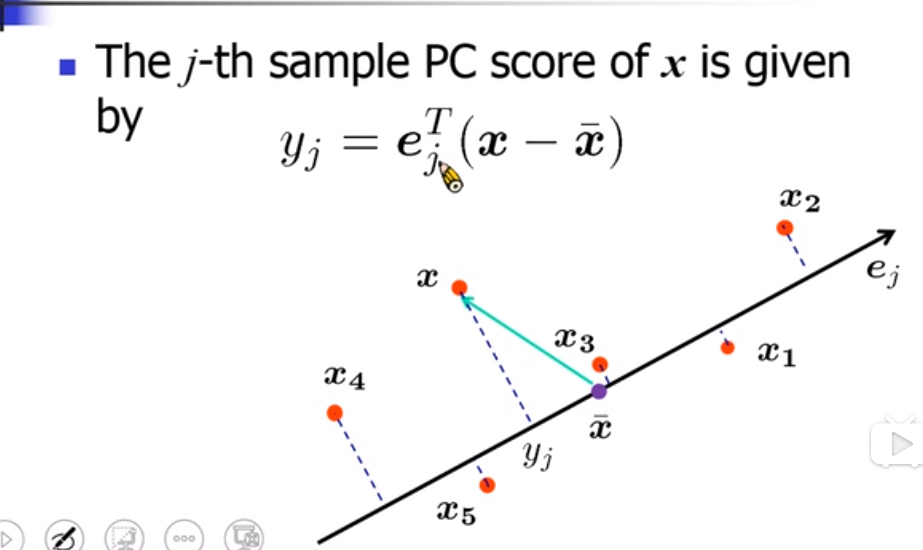
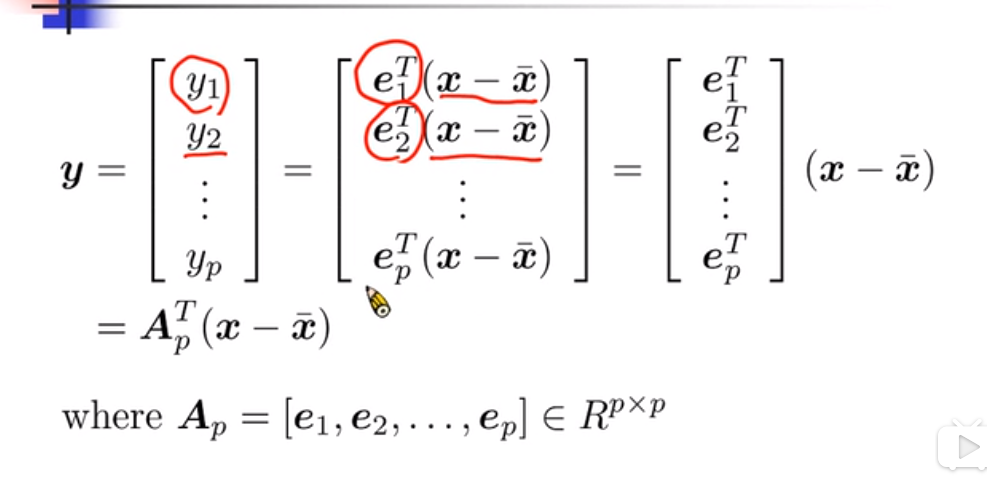
 y的分量一次减小

 

砍到只剩下yt  个

 

 

 

 

 

 

 

  

 

 

 

 

 

 

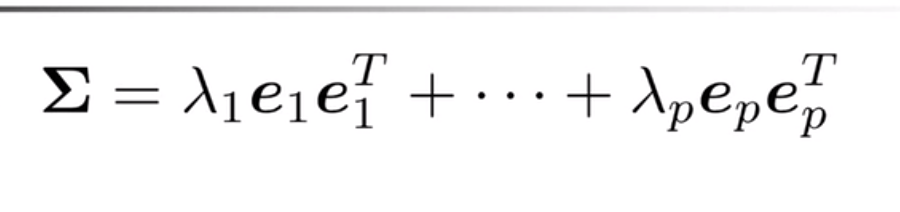
矩阵的对角线的和 是特征值之和

不知道要砍掉几个特征值

 

 

 

 

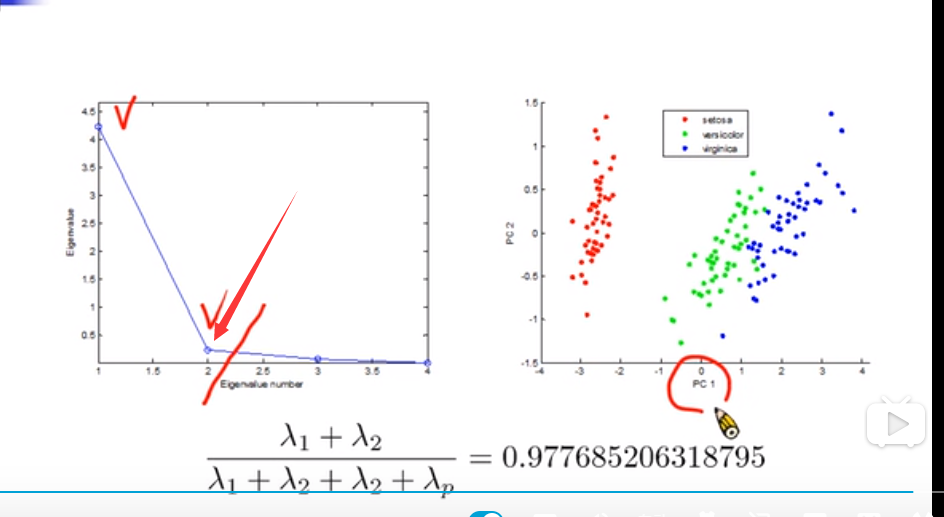
在手肘处砍掉

 

 

 

 

 

 

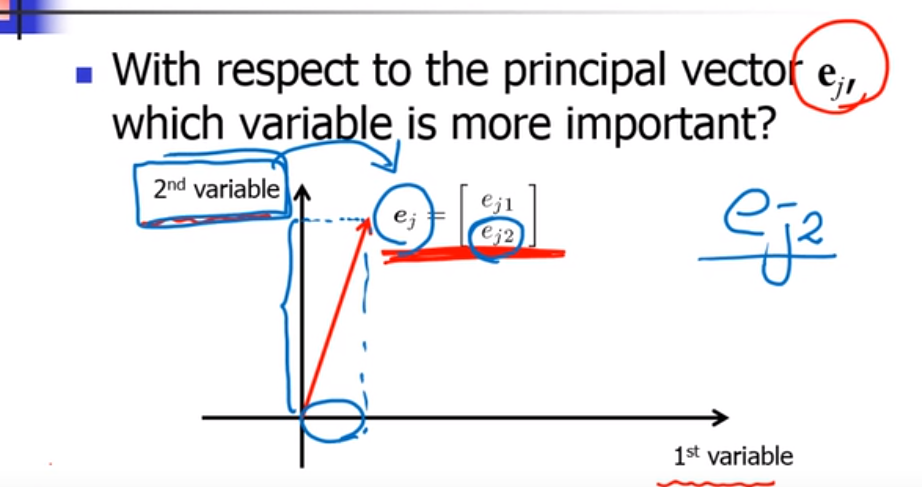
 e 中元素那个大，就哪个重要

 

 

 

 

 

 

 

 

 

 

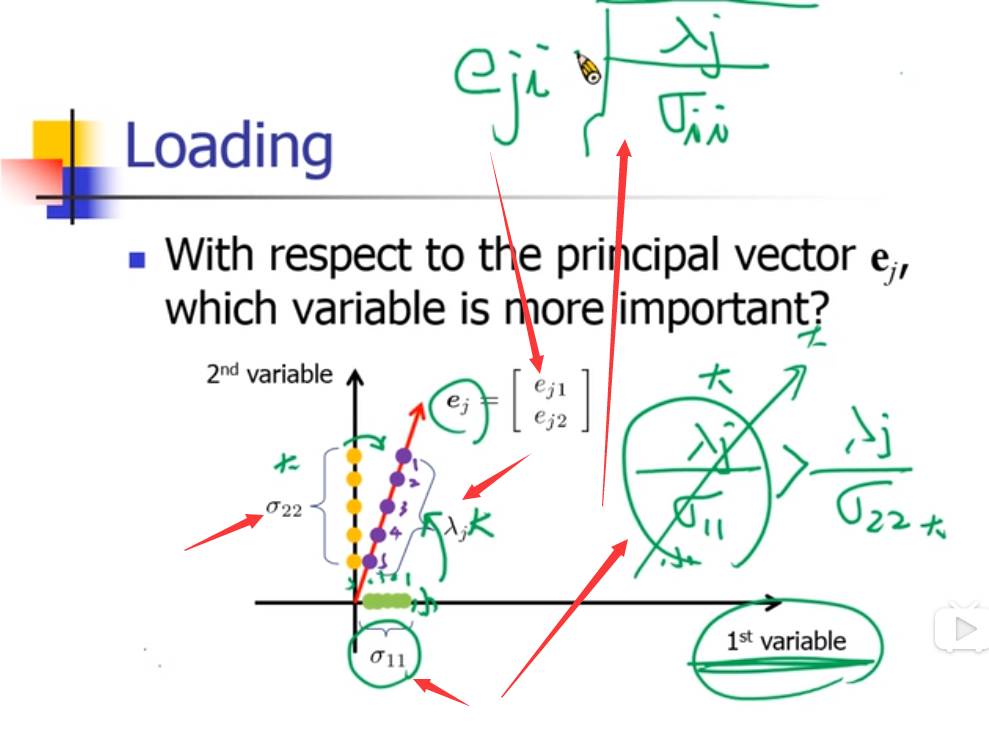
 xn 投影到第i个主轴  就是yni  

投影后平均下来是0 

 

 

 

 

 

 而且

 

 

 

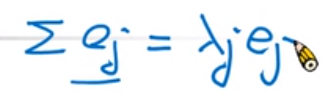
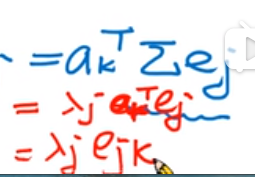 ejk   ej 的主轴第k个位置

 

 

 

 

 

 

 

转载于:https://www.cnblogs.com/china520/p/10634260.html