软件工程第二次作业

一. 选择开发工具

开发工具我们选择的是visual Studio，并使用c++进行开发，我使用的是visual Studio2019社区版。

启动界面



创建工程界面

二. 练习自动单元测试

我使用的测试工具是VSTS，测试步骤如下：

1 编写代码，

我写的是简单的求解最大公约数程序，代码如下

    #include <iostream>
    using namespace std;

    int yue(int a,int b) {
        int t;
        if (a < b){
                t = a;
            a = b;
            b = t;
         }
        while (b != 0){
                t = a % b;
            a = b;
            b = t;
        }
        return a;
    }

    int main() {
        int x, y;
        cin >> x >> y;
        int z = yue(x, y);
        cout << z;
        return 0;
    }

头文件：

#pragma once
int Yue(int a, int b) {
    int t;
    if (a < b) {
        t = a;
        a = b;
        b = t;
    }
    while (b != 0) {
        t = a % b;
        a = b;
        b = t;
    }
    return a;
}

2 创建测试程序

1. 右键解决方案 -> 添加 -> 新建项目 ->测试 -> 本机单元测试项目
   
   
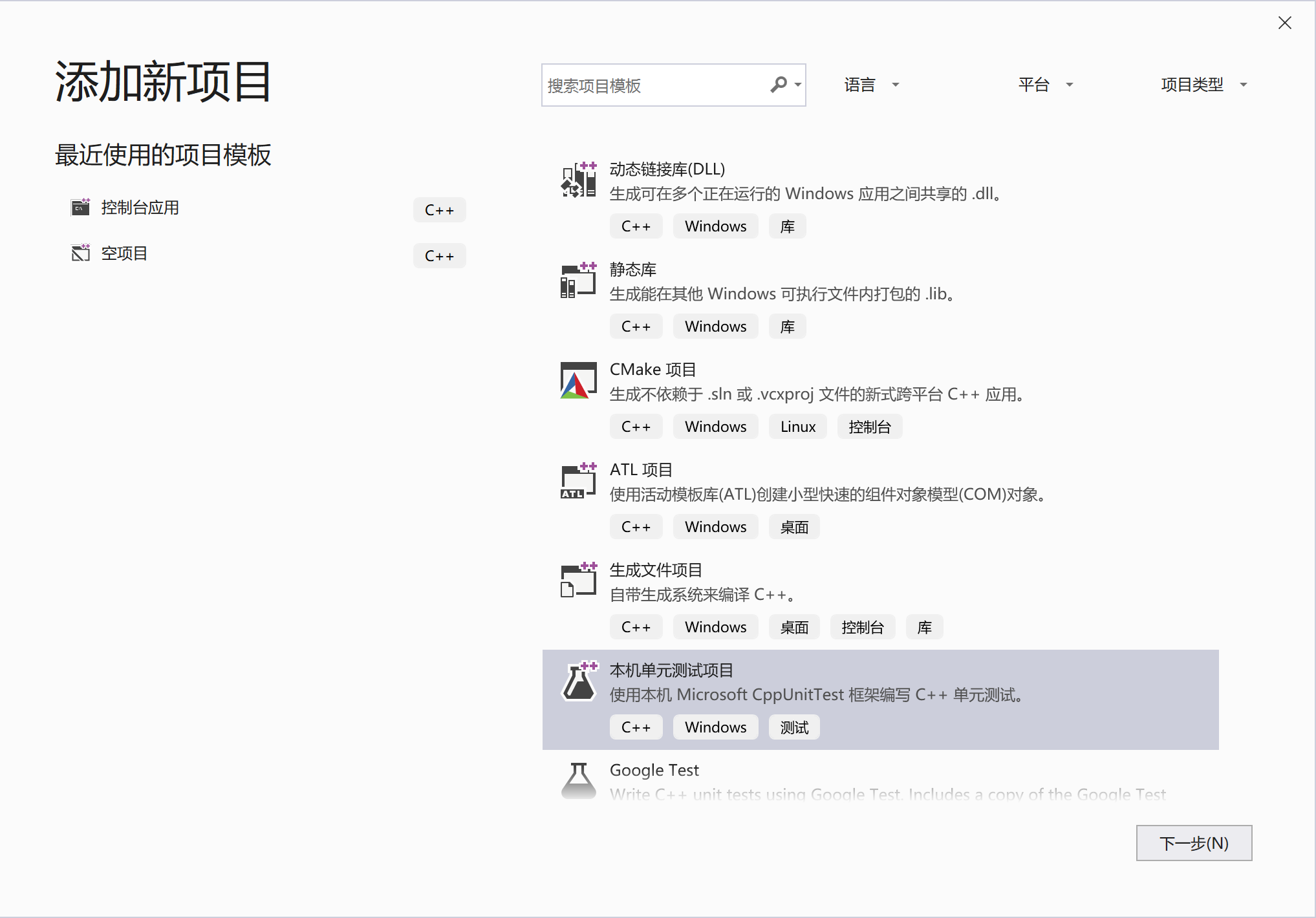
   创建本机单元测试项目
   
2. 将测试项目test222添加到引用
   
   
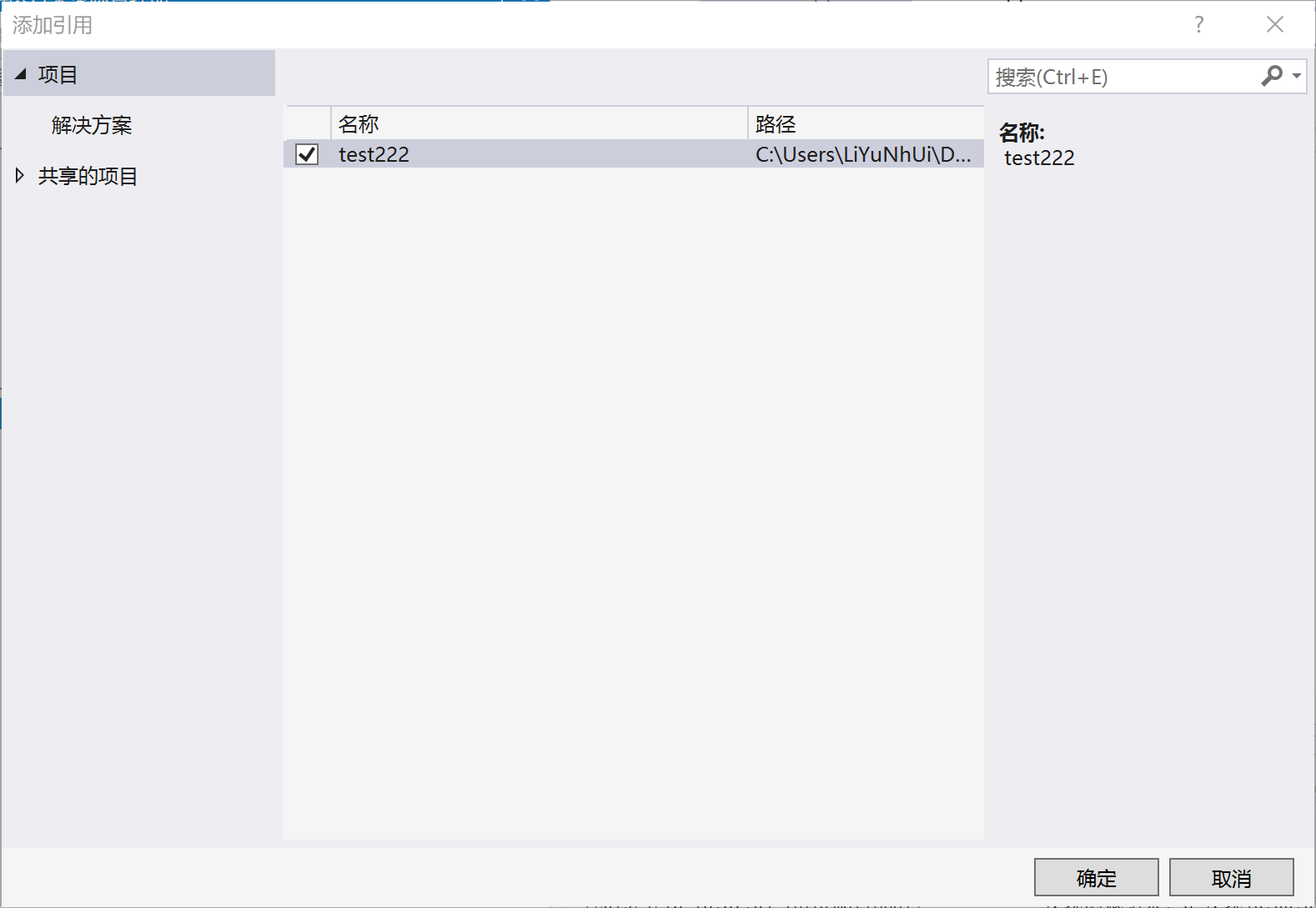
   添加引用
   
3. 添加附加依赖项
   
   
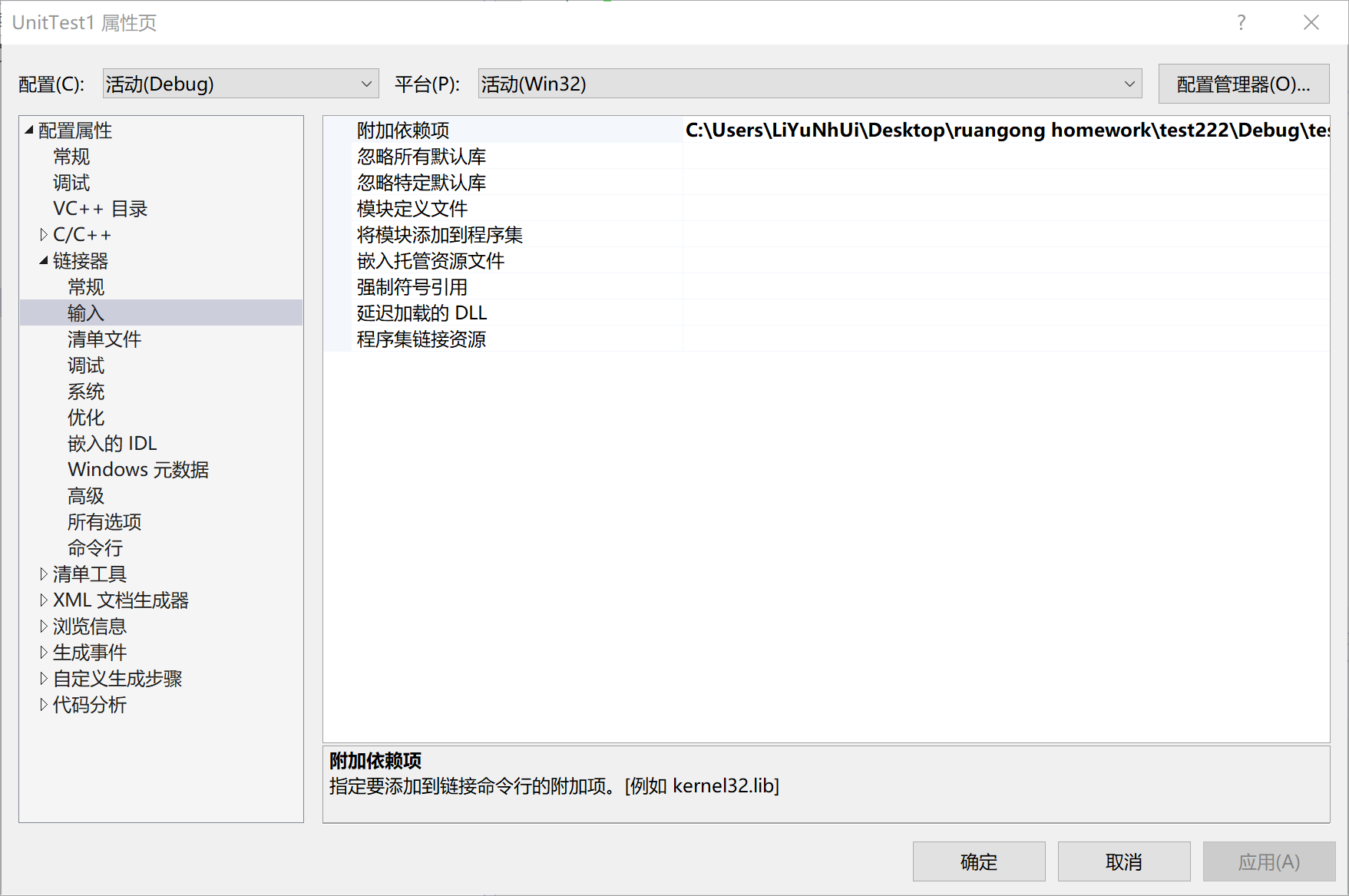
   添加附加依赖项
   
4. 编写测试程序，具体代码如下：

#include "pch.h"
#include "CppUnitTest.h"
#include"..\test222\test.h"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest2
{
    TEST_CLASS(UnitTest2)
    {
    public:
        
        TEST_METHOD(TestMethod1)
        {
            int x = 1, y = 1;
            int z = Yue(x, y);
            Assert::AreEqual(1, z);
        }
        TEST_METHOD(TestMethod2)
        {
            int x = 2, y = 1;
            int z = Yue(x, y);
            Assert::AreEqual(1, z);
        }
        TEST_METHOD(TestMethod3)
        {
            int x = 1, y = 2;
            int z = Yue(x, y);
            Assert::AreEqual(1, z);
        }

    };
}

测试样例1	测试样例2二	测试样例3
两数相等	前数大于后数	后数大于前数

测试结果如下：

测试结果

可见测试结果均为正确。

转载于:https://www.cnblogs.com/Pith/p/10700038.html