LeetCode题解

题目是这样的：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

 

 

例如：

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

 

 

 

输入: m = 7, n = 3
输出: 28

 

 

  这道题其实跟那个踩阶梯的题很相似：“假如有10步台阶,一次可走一步或两步，那么要走到达台阶顶,有几种走法，我们都知道，这个是斐波那契问题，递归就可以了”。

  我们可以这么解，假设最后一格是a[m][n],那么能到达a[m][n]的只有a[m-1][n]和a[m][n-1]。同理，要到达a[m-1][n],也只能从a[m-1-1][n]和a[m-1][n-1]；

要到达a[m][n-1],也只能从a[m-1][n-1]和a[m][n-1-1]，这是个递归问题。直到a[i][j]中i=1或者j=1,当i=1时，就只可以能时从a[i][j-1]到达，当j=1时，同样，也只能从a[i-1][j]到达；

于是，递归的边界找到了。

  可能上面说的不直观，请看下面:

```

           r(m,3)的值       r(m,4)的值   r(m,4)-r(m-1,4)的差值

            r(1,3)=1         r(1,4)=1         3

            r(2,3)=3         r(2,4)=4         6 

            r(3,3)=6         r(3,4)=10       10

            r(4,3)=10        r(4,4)=20       15  

            r(5,3)=15        r(5,4)=35       21  

            r(6,3)=21        r(6,4)=56       28  

            r(7,3)=28        r(7,4)=84       36  

            r(8,3)=36        r(8,4)=120      45  

            r(9,3)=45        r(9,4)=165

        有没有发现

        r(9,4)=r(8,4)+45=r(8,4)+r(9,3)=r(7,4)+r(8,3)+r(8,3)+r(9,2)

        r(8,4)=r(7,4)+36=r(7,4)+r(8,3)=r(6,4)+r(7,3)+r(7,3)+r(8,2)

        .

        .

        .

        .

        .

```

于是我们很快想到了递归函数怎么写：

```

    public int uniquePaths2(int m, int n) {

        if (m == 1) {

        return 1;

        }

        if (n == 1) {

        return 1;

        }

        return uniquePaths2(m - 1, n) + uniquePaths2(m, n - 1);

    }

```

运行一下：

 

 

结果对了，现在把参数值变大一点：

 

时间还凑合，再变大，这次运行时间有点久了：

 

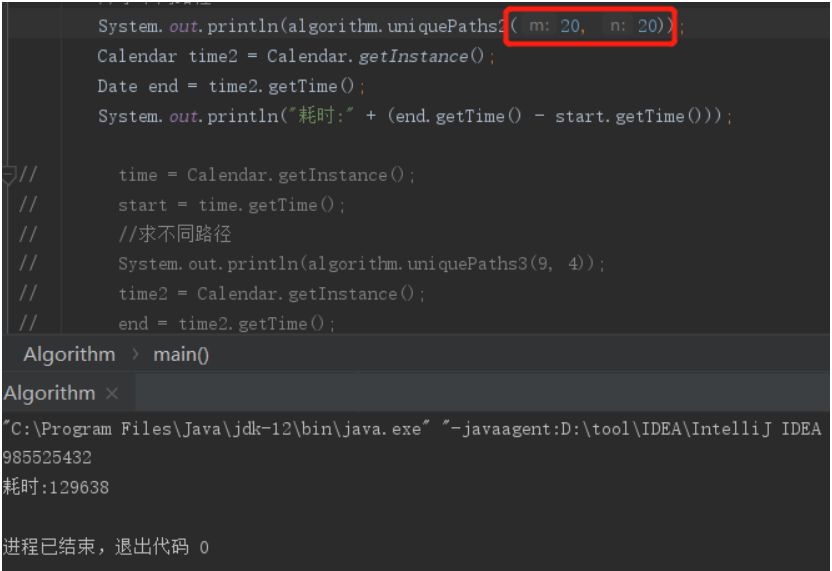
超过了两分钟！

为什么呢，请看上面的发现那里：在我们计算r(9,4)的时候是不是中间会计算两次r(8,3),并且r(8,4)和r(9,4)中间都会有r(7,4)的计算，而这些重复计算是很浪费时间的。对这块不了解的可以看这篇文章： https://mp.weixin.qq.com/s/llvtdxaPc29CNkcmtPHxKw

于是，为了避免重复计算，这个函数需要改写，我们可以这样，在计算r(8,3)的时候把r(8,3)的值保存起来，这样下次计算r(8,3)的值的时候可以直接获取，不需要再计算了，根据这个思路，把算法改良一下：

```

public int uniquePaths3(int m, int n) {

        int[][] all = new int[m][n];

        for (int i = 0; i < m; i++) {

            for (int j = 0; j < n; j++) {

                if (i == 0 || j == 0) {

                    all[i][j] = 1;

                } else {

                    all[i][j] = all[i - 1][j] + all[i][j - 1];

                }

            }

        }

        return all[m - 1][n - 1];

}

```

再看看运行结果：

 

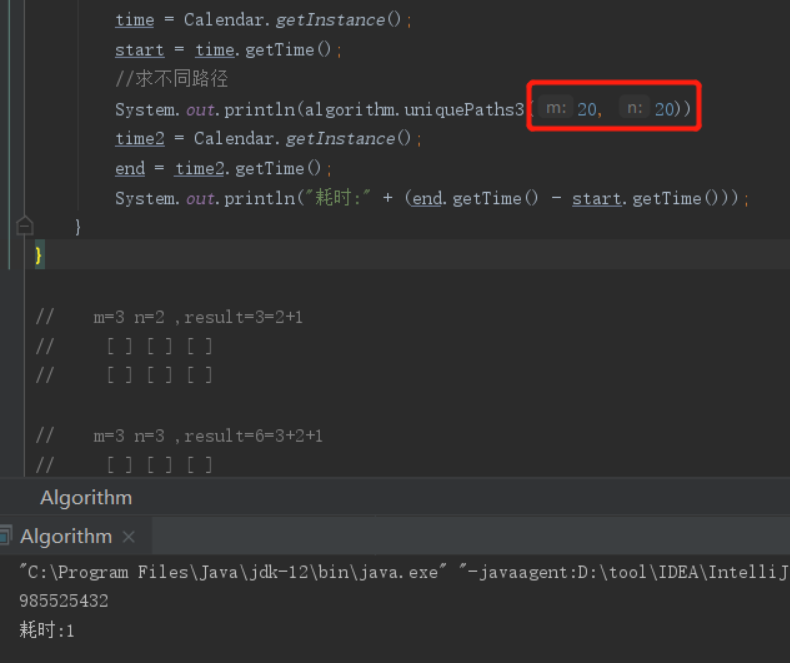
快了好多是不是！

转载于:https://www.cnblogs.com/aibaofeng/p/11098525.html