

下面是机器学习的《监督式学习》课程的一篇试读文章,进行了一下重新排版,然后展示在这里。由于格式的限制,缺少了一些习题、可运行的代码、证明、注释等,可能会导致解释差强人意,所以介意的同学可以直接访问 线性回归与最小二乘,以获得最佳的阅读体验。
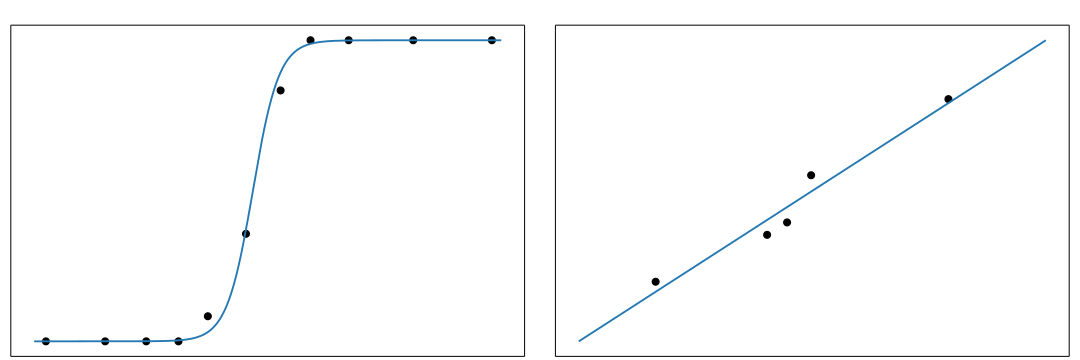
回归大致可以理解为根据数据集 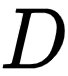 ,拟合出近似的曲线,所以回归也常称为拟合(Fit),像下列右图一样拟合出来是直线的就称为 线性回归:
,拟合出近似的曲线,所以回归也常称为拟合(Fit),像下列右图一样拟合出来是直线的就称为 线性回归:
下面就来解释其中的一些细节。
1 线性回归首先,为什么拟合曲线会被称为回归呢?1.1 均值回归
“回归”这个词源于弗朗西斯·高尔顿爵士(英文:Sir Francis Galton,1822年2月16日-1911年1月17日):

他发现高个子父亲的儿子身高会矮一些,而矮个子父亲的儿子身高会高一些(否则高个子家族会越来越高,而矮个子家族会越来越矮),也就是说人类的身高都会回到平均值附近,他将这种现象称为 均值回归 。
1.2 线性回归
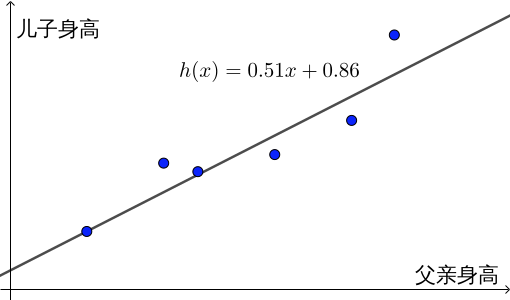
高尔顿的研究过程用现在的数学语言来表述就是,首先对一些父子的身高进行了抽样,得到数据集 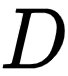 ;然后根据数据集拟合出一条直线;最后通过该直线就可以对某父亲
;然后根据数据集拟合出一条直线;最后通过该直线就可以对某父亲 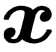 的儿子的身高进行预测了:
的儿子的身高进行预测了:
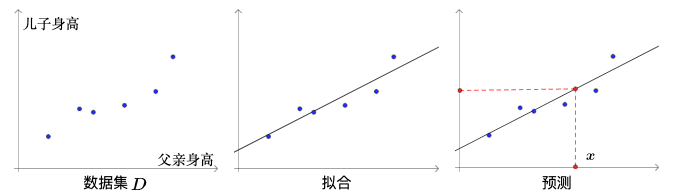
高尔顿拟合的直线方程为(单位为米):
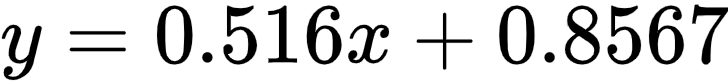
将方程和 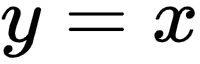 联立,可得:
联立,可得:
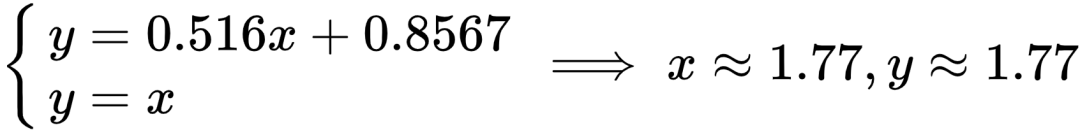
也就是说这两条直线会交于点 (1.77, 1.77),这说明身高低于1.77米的父亲,他的儿子身高会高一些;而高于1.77米的父亲,他的儿子身高会矮一些:
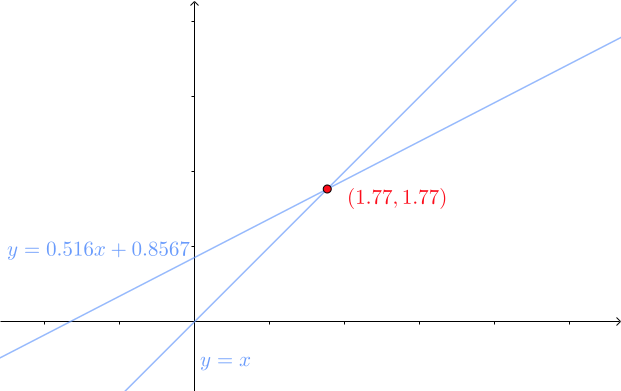
所以这条拟合出来的直线,其实就表示了均值回归现象,因此拟合直线的过程被称为 线性回归(Linear Regression)。
2 经验误差函数下面开始解释高尔顿是如何根据数据集来拟合直线的。先来介绍下线性回归的经验误差是什么。2.1 假设空间 
首先肯定是用直线来进行拟合:
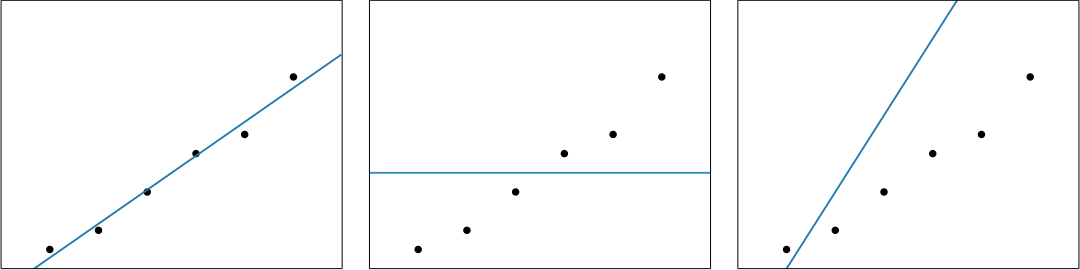
所以假设空间为:
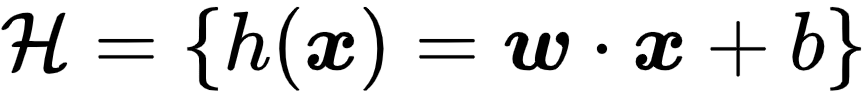
和感知机的假设空间差不多,只是少了  函数。
函数。
2.2 数据集 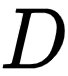
在历史上,高尔顿总共采集了近千个父子身高的数据来拟合。本课为了方便讲解,我们从中抽取了六个(原始数据的单位是“英寸”,这里全部转为了“米”)作为数据集 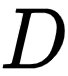 :
:
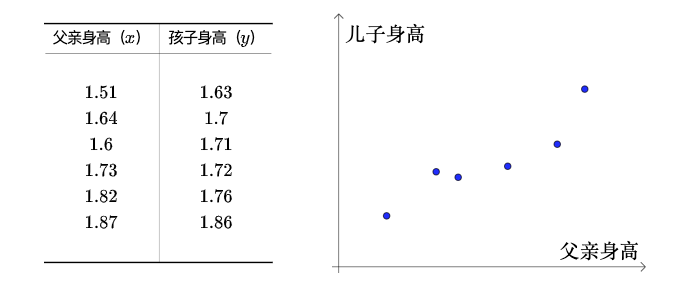
2.3 经验误差
随便找一条假设空间中的直线 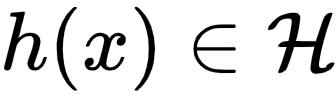 ,对于某父亲身高
,对于某父亲身高 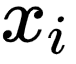 ,该直线给出的
,该直线给出的 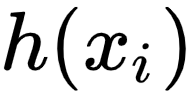 和真实的儿子身高
和真实的儿子身高 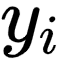 是存在距离的,这个距离也称为点与直线的误差,高尔顿用两者差的平方来表示
是存在距离的,这个距离也称为点与直线的误差,高尔顿用两者差的平方来表示 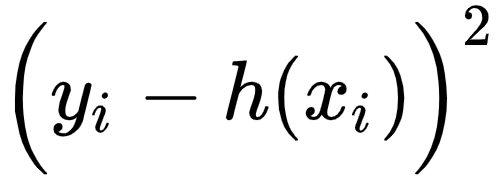 :
:
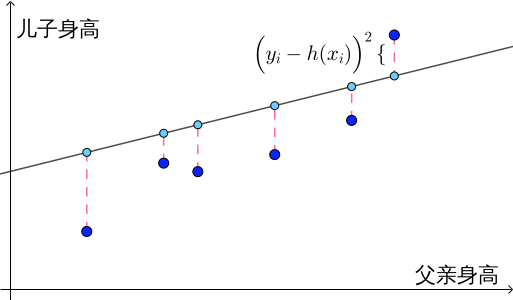
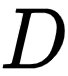 中所有点与该直线的误差加起来,再进行算术平均就是该直线在数据集
中所有点与该直线的误差加起来,再进行算术平均就是该直线在数据集 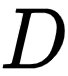 上的经验误差:
上的经验误差: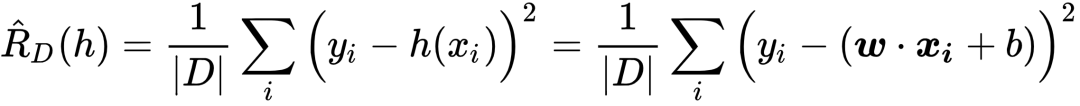 其中
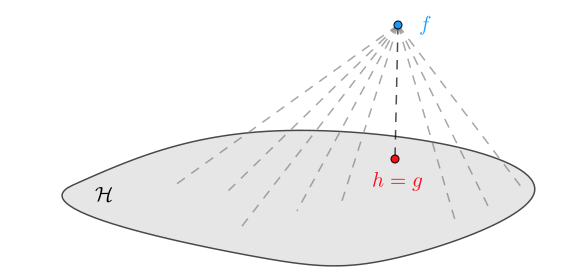
其中 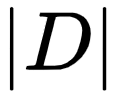 表示该数据集的大小。3 最小二乘法有了经验误差函数之后,就可以利用上一单元介绍的经验误差最小原则来设计算法,从而在假设空间
表示该数据集的大小。3 最小二乘法有了经验误差函数之后,就可以利用上一单元介绍的经验误差最小原则来设计算法,从而在假设空间 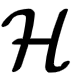 中挑选离
中挑选离 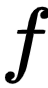 最近的
最近的 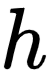 作为
作为 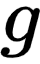 :
:
具体到线性回归中,其经验误差函数为:
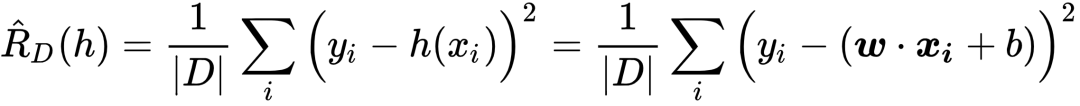
根据经验误差最小原则,只需要求出使得该经验误差函数取得最小值的 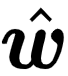 和
和 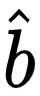 :
:
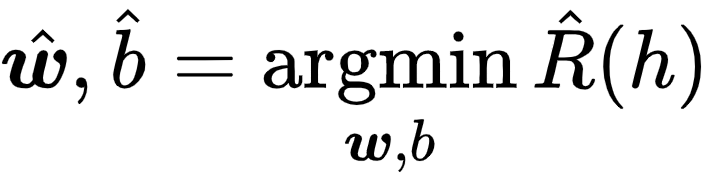
实际上就得到了离 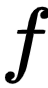 最近的
最近的 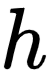 ,本节就来介绍如何求解
,本节就来介绍如何求解 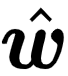 和
和 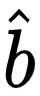 。
。
3.1 凸函数
首先,将手上的数据集 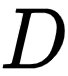 :
:
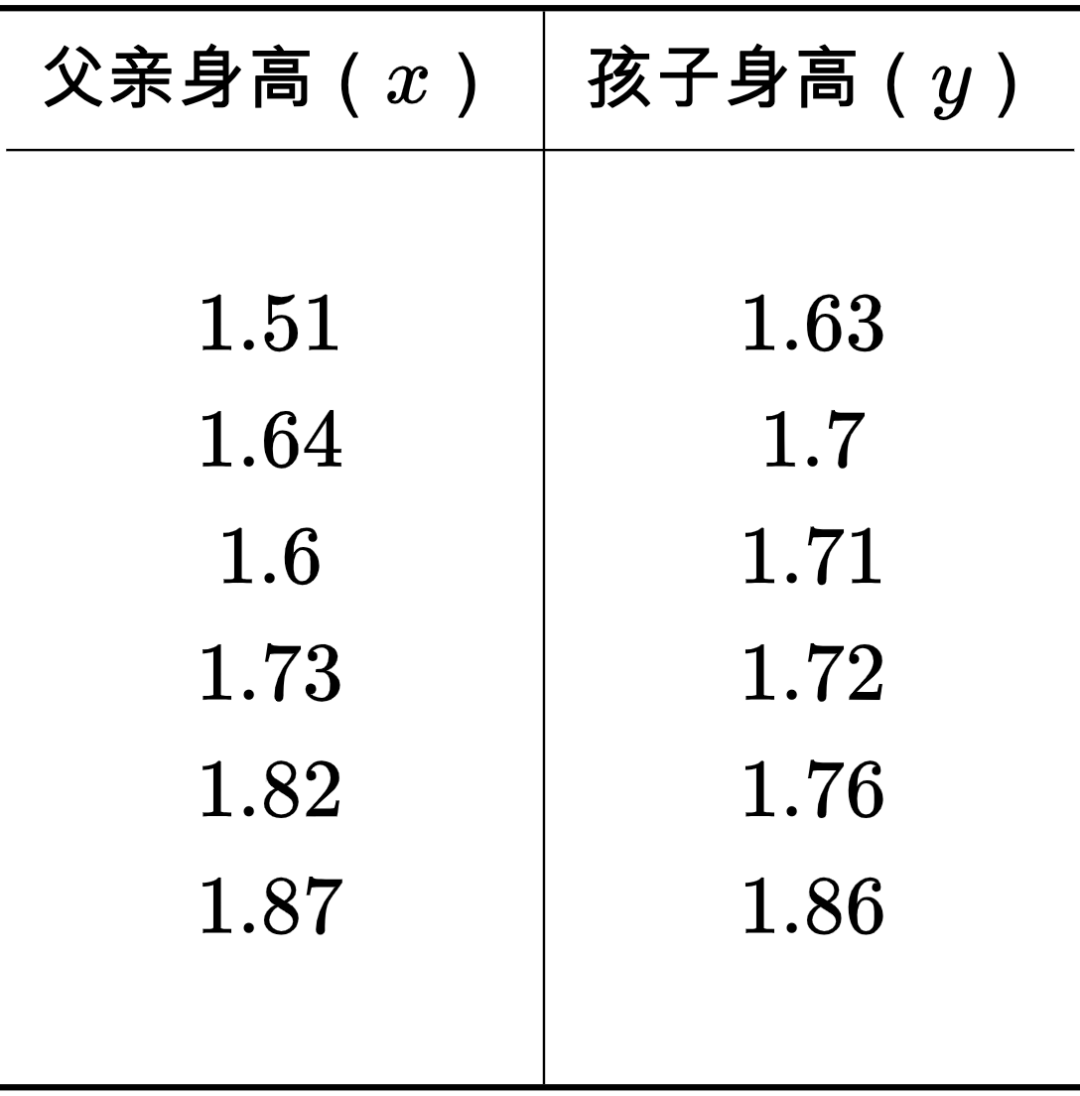
代入线性回归的经验误差函数后可得:
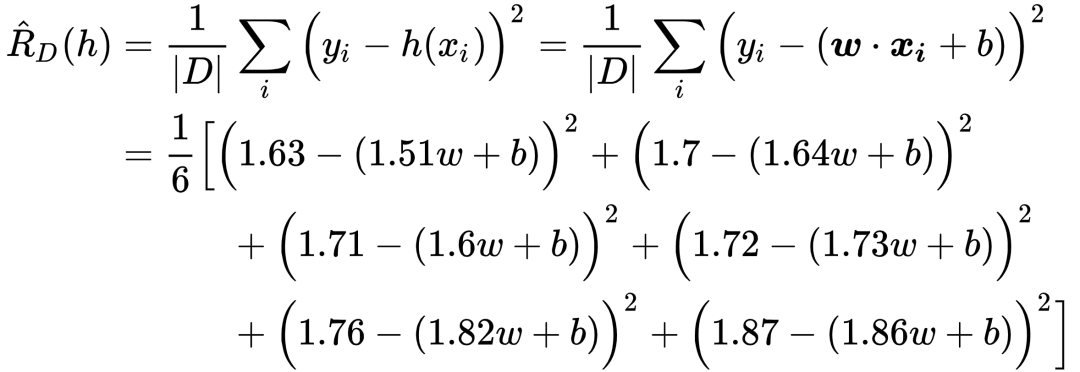
可见 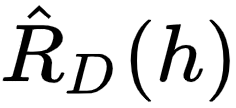 是关于
是关于 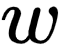 和
和 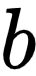 的函数,并且是 凸函数(Convex Function)。凸函数意味着画出来看上去像山谷:
的函数,并且是 凸函数(Convex Function)。凸函数意味着画出来看上去像山谷:
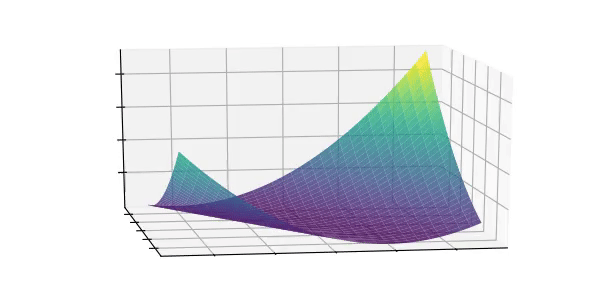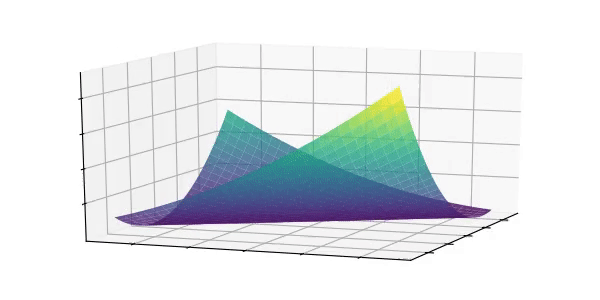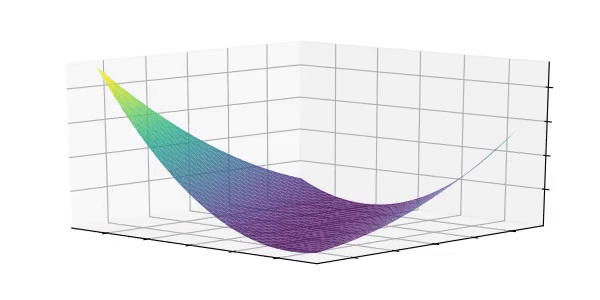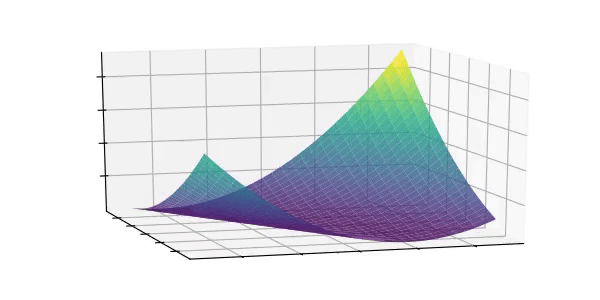
3.2 凸函数的最小值
就如山谷肯定有最低点一样,凸函数肯定有最小值,这说明最小值是一定存在的。并且凸函数更重要的性质是,使得经验误差函数 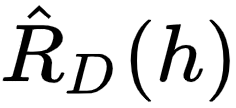 取得最小值的
取得最小值的 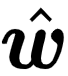 和
和 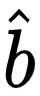 ,可以通过求解下面方程组得到:
,可以通过求解下面方程组得到:
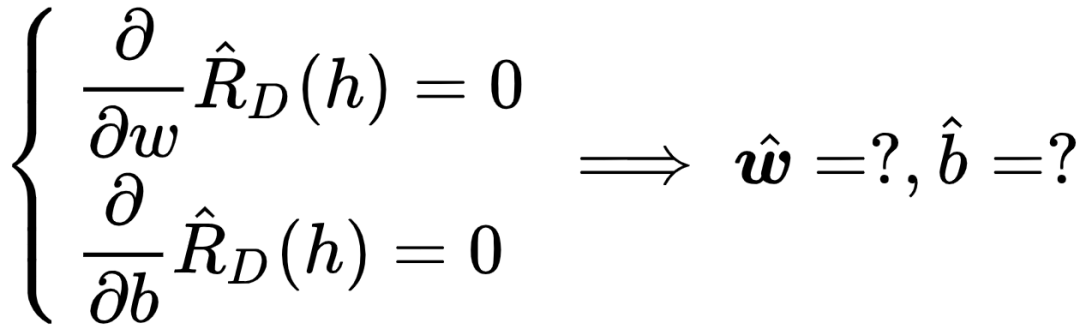
因为线性回归的经验误差函数 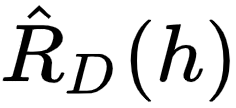 是平方之和,所以本节介绍的求解该经验误差函数的最小值的方法被称为 最小平方法 ,国内各种教材中也常称为 最小二乘法 。
是平方之和,所以本节介绍的求解该经验误差函数的最小值的方法被称为 最小平方法 ,国内各种教材中也常称为 最小二乘法 。
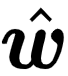 和
和 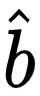 :
:from sympy import symbols, diff, solveimport numpy as np# 数据集 DX = np.array([1.51, 1.64, 1.6, 1.73, 1.82, 1.87])y = np.array([1.63, 1.7, 1.71, 1.72, 1.76, 1.86])# 构造经验误差函数w, b = symbols('w b', real=True)RDh = 0for (xi, yi) in zip(X, y): RDh += (yi - (xi*w + b))**2RDh *= 1/len(X)# 对 w 和 b 求偏导eRDhw = diff(RDh, w)eRDhb = diff(RDh, b)# 求解方程组ans = solve((eRDhw, eRDhb), (w, b))print('使得经验误差函数 RD(h) 取最小值的参数为:{}'.format(ans))上面代码运行后,可以解出 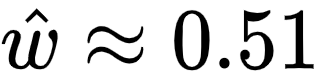 以及
以及 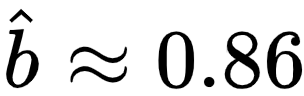 ,得到的结果和高尔顿几乎一样:
,得到的结果和高尔顿几乎一样:
我们通过通俗易懂、图形化的方式,对机器学习中的...【来源】马同学高等数学。

【推荐阅读】
高中数学及中学教育优秀文章选读(许兴华数学)
中科院院士:为什么要学数学?
韩树:一道高三模拟考导数题的几种解法
张小明——平凡恒等式应用两例
王芝平:有心圆锥曲线的切线性质新探
【精品珍藏】 高考数学解题36计
陕西省西安中学2019-2020学年度第一学期期中考试高一数学试题
杨宪伟——用12种方法求多元函数的最值:榆林十中数学教研组会教研成果之一
袁振国:教育规律与教育规律研究
张恭庆:数学与国家实力
赵振华——无意的探索:命中2020年高考真题
高中数学的十大函数解题方法!
【高考神话】衡水中学传奇,大家瞧瞧神话背后的成功秘诀是什么?
杨东平:应该坚决打击超级中学的现象
高中数学竞赛50讲:第29讲 数学归纳法应用中的命题转换云南师大附中2021届高三高考适应性月考卷一理科数学试题
许兴华——高一数学中的对数与对数函数学习指导
火了! 轰动清华! 开学典礼上发言的新生代表到底什么来头? 太优秀了吧!
专家田刚,朱华伟等学者热议中国数学教育的困境与出路ooo从取消高考选择题改起!)
陈煜——2020年全国高中数学联赛加试题的解答
高一数学必修一综合检测试卷
【高考研究】平面向量“三点共线定理”的妙用--带你深入理解其本质!
【数学美】神奇的动态图——让你瞬间爱上数学!
【高考数学】研究高考题 寻找命题点
2020中国数学奥林匹克希望联盟夏令营第一天之试题解答
北大学长经验独家分享:我是如何战胜高中数学偏科的?
【教学研究】20类122条做法,泄露了正高级教师高效课堂的天机
合肥市2021届开学调研文理试题及答案+贵州省贵阳市2021届高三上学期8月摸底考试试题及答案
任子朝等 | 高考文理不分科后数学科考试内容改革研究
【高考研究】突破圆锥曲线大题的十个大招(一)
高考研究】突破圆锥曲线大题的十个大招(二)
三角变换中“巧变角”的常见模型
平面解析几何的思维特征与研究方法
陈煜—— 高中数学联赛加试漫谈
2021届考生必看: 一轮复习4大方法+30则经验总结+5大坏习惯!
对数均值不等式在高考及竞赛中的运用
陈煜——数学竞赛中的代数问题选讲
【教育文摘】看见孩子是教育的出发点
【高考百日冲刺系列.数学全集】第1集~第23集合集(许兴华数学)
传遍大江南北的对数均值不等式
高中数学竞赛50讲:第22讲 利用直线束和圆解题
衡水中学1700字2020年新学期入学须知及录取通知书曝光! 禁用手机/规定发型…
【数学世界】非常全面的数学各个分支简介
高一数学:函数综合测试试卷与详解
高中数学难点突破 | 立体几何中最值问题全梳理
高中数学不等式专题全攻略---应有尽有,果断收藏!
高中专题复习||函数的对称性与周期性
@准大学生:大学开学最全物品清单在这里!快收藏备用
【教师珍藏】批改作业的100例精彩评价语言,直接可以拿来用!
高一数学:函数综合练习题精选(更正版)
圆锥曲线经典问题精编共23题
老师需要修炼的10项教学基本功,对你的职业生涯很重要!
平面向量中极化恒等式的迁移应用
50条高考数学秒杀公式+方法,助你再提30分!
【高中数学】利用函数表达式确认函数图像的这五大技巧,你都掌握了吗?
高中数学的四个刷题误区, 让你的成绩惨不忍睹! 一篇文章拯救你!
高中数学中简化解析几何运算的5个技巧
【震惊】一所县城中学刷屏,11人超过700分!凌晨校园照震撼无数家长!
毛坦厂中学高考放榜, 再次刷爆网络! 改变命运的梦想, 都有挡不住的光芒!
2020年人教版高中新教材网络培训会开班式
2020年人教版高中数学新教材总体介绍利用导数研究不等式问题
高一数学:函数的奇偶性及相关简单应用
袁亚湘院士《数学漫谈》讲座课件
林琳——用配方法解两道数学最值题
高中数学:数列递推公式的9种常见模型
初中与高中数学衔接教材(上)ooo全面完整版
初中与高中数学衔接教材(下)ooo全面完整版
对2018年高考全国卷Ⅰ理科数学解析几何试题的拓展探究—兼谈核心素养下圆锥曲线的备考
高考数学辅导:构造函数法证明不等式的六种策略
【教研撷萃】高考中圆锥曲线解答题的研究方向
高一数学:函数单调性的简单应用
【培训提高】放假了!教师如何写好教学反思?值得所有教师收藏!
大学你适合读数学专业吗?北京某大学老师为你提示数学专业的秘密!(上)
大学你适合读数学专业吗?北京某大学老师为你提示数学专业的秘密!(下)
高中数学中的八种构造对偶式解题方法
2020高考志愿填报参考:数学专业大学排名,数学专业的就业方向
考得好不如志愿填得好 | 一篇文章教你填报完美的大学!附:“最权威”全国普通高等学校名单
700分以上学霸激增!2020年高考哪个省最强?
高考速递:十五省公布高考录取分数线(附填报志愿链接)

【投稿须知】公众号《许兴华数学》诚邀全国各地中小学数学教师、教研员和数学爱好者热情投稿!来稿时请注意以下五点:
(1)来稿请注明真实姓名、工作单位、联系方式(无具体工作单位和真实姓名的投稿,一般都不会采用)。
(2)来稿一般要求同时用word文档和PDF格式的电子稿件(防止不同版本的Word打开时出现乱码)。另外,也接受少数著名教师的手写稿(手写稿必须清晰可读)。
(3)每篇文章请认真审查复核,防止错误发生,来稿文责自负。如有抄袭,则有可能被举报并受到有关著作版权部门的追责。
(4)投稿邮箱:chinamatha@163.com;或加主编微信xuxinghua168投稿.(5)本公众号对优秀作者和名师一般会附上“作者简介”,以让广大读者更好地了解作者的研究成果和方向,以便进一步学习作者的相关数学思想或解题方法。





 这篇博客解释了线性回归的概念,起源于弗朗西斯·高尔顿的均值回归现象研究。线性回归通过拟合数据集来找出近似直线,描述了身高等属性如何趋向于平均值。文章介绍了线性回归的假设空间、经验误差函数以及最小二乘法的应用。
这篇博客解释了线性回归的概念,起源于弗朗西斯·高尔顿的均值回归现象研究。线性回归通过拟合数据集来找出近似直线,描述了身高等属性如何趋向于平均值。文章介绍了线性回归的假设空间、经验误差函数以及最小二乘法的应用。
















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








