html5 绘制,Html5 绘制N角形

转载自：

http://www.zybang.com/question/0bb53a7133bd38703648c478d598209e.html

代码如下：

function createStar(context,n,dx,dy,size)

{

context.beginPath();

var dig = Math.PI / n * 4;

for(var i=0;i

{

var x = Math.sin(i*dig);

var y = Math.cos(i*dig);

context.lineTo(x*size+dx,y*size+dy);

//alert(x*size+dx);

//alert(y*size+dy);

}

context.closePath();

}

var canvas = document.getElementById('mc');

var ctx = canvas.getContext('2d');

createStar(ctx,3,60,50);

ctx.fillStyle="#f00";

ctx.fill();

createStar(ctx,5,160,7,260,50);

ctx.fillStyle="#f00";

ctx.fill();

ctx.fillStyle="#f00";

ctx.fill();

createStar(ctx,9,360,50);

ctx.fillStyle="#f00";

ctx.fill();

程序可以改动一下，看起来会更容易一点。

// 开始创建路径

context.beginPath();

var dig = Math.PI / n * 4;

//改：var dig = 2*(2*Math.PI / n) ;

//括号里就是将360度平均分成n份

//为什么前面还要乘以2，见下面(2.画这类图形的技巧(或者说规律。))

for(var i = 0; i < n ; i++)

{

var x = Math.sin(i * dig);

var y = Math.cos(i * dig);

context.lineTo(x * size + dx,y *size + dy);

//上面三行改成：

//var x = dx+size*Math.sin(i *dig);  //(1)

//var y = dy+size*Math.cos(i *dig);  //(2)

//context.lineTo(x,y);

//(1)，(2)其实是圆的参数方程

//把(1)，(2)再改，如下：

//varx=dx+size*Math.cos(Math.PI/2-i*dig);//sin变cos

//vary=dy+size*Math.sin(Math.PI/2-i*dig);//cos变sin

}

context.closePath();

首先至少掌握三点知识。

1.这类图形的特点。

2.画这类图形的技巧(或者说规律。)

3.圆的参数方程。

变量：

n:N角星的顶点数。

dx,dy: N角星的位置，也是N角星中心点的坐标

size: N角星的大小，也是N角星任一顶点到N角星中心点的距离。

angle: 相邻顶点到中心点形成的夹角度

dig: 每一段两点顶点与中心点形成的夹角度

1.这类图形的特点。

特点：

(1)所有的顶点都在一个圆上。圆心O为图形的中心点，半径r为中心点到任一顶点的距离,即size。

(2)任意相邻的两个顶点到中心点所形成的角度相等。则angle=2*PI/n：

2.画这类图形的技巧(或者说规律。)

你给的程序画出来的图形，每画一条线段之间跳过了一个顶点。

举个例子，拿七角星来讲，首先先给七角星的顶点按顺时针编号，即1-7。

你给的程序是这么连的：1-3-5-7-2-6-4-6-1,

跟据这点，可得出一个规律：

1-3-5-7-2-6-4-6-1，这个数列，每相邻的两点与中心点形成的角度相等。

即1-3，3-5...形成的角度相等，这个角度即是dig=2*angle。

如果改成dig=angle的话，也就是说

var dig = Math.PI / n * 4;那么画出来的图形如下：

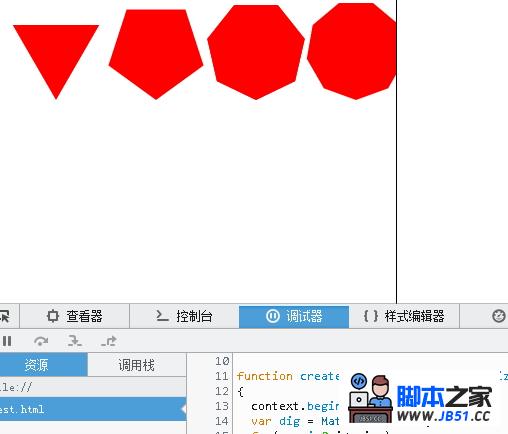
3.圆的参数方程.

方程如下：(x0,y0)为中心点的坐标。即(dx,dy)，a为角度，r为半径即size

x=x0+r*cos(a);

y=y0+r*sin(a);

举个例，画7角星：

从0度的点开始画：按1-3-5-7-2-6-4-6-1画,

那么，

第1点：x=dx+size*cos(0);y=dy+size*sin(0);

第3点：x=dx+size*cos(0+dig*1);y=dy+size*sin(0+dig*1);

第5点:x=dx+size*cos(0+dig*2);y=dy+size*sin(0+dig*2);

...

表达有限，比较凌乱，哈哈。

根据这个原理，我写出下面的函数，画出来的星形比较“骨感”：

//参数的意思与你给出来的一样。

//注，num不能为偶数，否则画出来的不是星形

function drawStar(pan2d,num,x,y,size)

{

pan2d.beginPath();

var startAngle=-Math.PI*0.5;// 起点角度

var dig=Math.PI-Math.PI/num;//vardig=Math.PI-2*Math.PI/num*0.5;

for(var i=0;i

{

varangle=startAngle+dig*i;

var px=x+size*Math.cos(angle);

varpy=y+size*Math.sin(angle);

pan2d.lineTo(px,py);

}

pan2d.closePath();

pan2d.stroke();

}

△注意：

sin函数取弧度，不止取角度